20. yüzyılın en etkili matematikçi, mantıkçı ve filozoflarından biri olan Bertrand Russell, modern dönemin en ünlü ve etkili mantıksal paradokslarından birine adını vermiştir. Bazı antik paradokslar, mantık veya muhakeme problemleriyle ilgiliyken, Russell paradoksu küme kavramına odaklanmıştır. Bu makalede, bu paradoksu ve felsefe ile mantık üzerindeki sonuçlarını inceleyeceğiz.
Günümüzde kümeler konusunu okullarda öğretirken alışılagelmiş bir biçimde tanımıyla başlarız. Oysa ki küme de tanımsız bir terimdir. Yaygın olarak bilinen “iyi tanımlanmış nesneler topluluğu” tanımı da sorunludur. Örneğin iyi tanımlanmış ne anlama gelir?

Matematikçi Georg Cantor ve diğer erken küme teorisyenleri, kümeler teorisini icat ederken, kümenin ne olduğu konusunda oldukça belirsiz bir fikirle yola çıkmışlardı. Georg Cantor‘’un “iyi tanımlanmış her nesneler topluluğu bir kümedir” tanımı da bir paradoksa yol açmıştır.
Matematik Tarihine Damga Vuran Russell Paradoksu Nedir?
Russell Paradoksu 1901’de Bertrand Russell tarafından ortaya çıkarılan ve küme teorisinin yeniden formüle edilmesini gerektiren bir paradokstur. Russell paradoksu İngilizcesi “naive set theory” olan sezgisel kümeler kuramı ile ilgilidir. Bu küme kuramı alışageldiğimiz aksiyomatik küme kuramından farklıdır.
Farkı kısaca özetlemek gerekirse aksiyomatik kuram adından da anlaşıldığı gibi mantık çerçevesinde biçimlenen aksiyomlar ile ilerler. Oysa ki sezgisel küme kuramı resmi olmayan tanımlamalar ile başlar. Bu küme teorisi, matematikçiler tarafından 19. yüzyılın sonunda geliştirilen orijinal küme teorisidir.
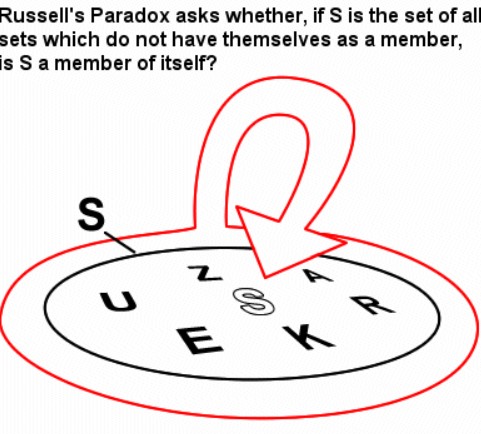
Bu bağlamda ele almamız gereken Russell Paradoksu hem kendilerinin üyesi gibi görünen hem de kendilerinin üyesi olmayan kümelerle ilgilidir. Matematikçilerin ve mantıkçıların kullandıkları terimlerle paradoksu size açıklamamız yazının anlaşılmasını zorlaştıracaktır. Bu nedenle Russell Paradoksu denildiği zaman akla gelen ilk örnek ile konuyu aktarmaya çalışalım.
Berber paradoksu, Bertrand Russell tarafından paradoksu örneklemek için kullanılmıştır. Köyün birinde bir berber varmış. Bu berber dükkanının önünde şöyle bir levha asılıymış “sadece kendini tıraş etmeyen erkekler tıraş edilir.” Yani bu berber o köydeki kendini tıraş etmeyen herkesi tıraş edermiş. Ancak kendini tıraş edenleri de tıraş etmezmiş. Peki ya berber? Berber tıraş olur mu?

Varsayalım ki berber kendini tıraş edenler arasında olsun, şayet böyle olursa levhaya göre ters bir durum ortaya çıkar. Levhaya göre berberin “kendini tıraş edenler” kısmında olması gerekmektedir. Ancak diğer grupta yani ” berbere tıraş olanlar” grubunda yer almaktadır. Her iki grupta da nasıl var olabilir? Aksi ifadeyi ele alacak olursak, berber, “kendini tıraş edenler” kısmında değil de “berbere tıraş olanlar” kısmında olsun. O zamanda yukarıdaki ifadeye benzer ters bir önerme karşımıza çıkacaktır.
Bu, doğrudan bir çelişkiye yol açar görünen bir durumdur, bir şeyin hem doğru hem de yanlış olduğunu söylemektir. Bir paradoksun yaptığı da budur. Russell’ın keşfettiği şey, bir küme kendinden söz ettiğinde bu tür bir paradoksun ortaya çıkacağıdır.
Russell’ın Paradoksuna, Gottlob Frege’nin Katkısı Nedir?

Aslında Bertrand Russell, Russell paradoksunu Alman matematikçi, mantıkçı ve filozof Gottlob Frege’nin çalışmasına bir yanıt olarak geliştirdi. Frege, 1884 tarihli aritmetiğin temelleri üzerine yazdığı eserinde (Die Grundlagen der Arithmetik, eine logisch-matematische Untersuchung über den Begriff der Zahl) ve 1893 yılında ilk ve tek cildini yayımladığı aritmetiğin temel yasaları hakkında yazdığı eserinde de (Die Grundgeseztze der Arithmetik), sayıların, saf mantıktan nasıl türetilebileceğini ortaya koymaya çalışmıştır.
Frege’nin geliştirmeye başladığı bu fikir, biçimsel mantığın gelişiminde de bir dönüm noktası olmuştur. Klasik mantık, “tüm” ve “bazı” gibi ifadeleri içeren önermelerin ele alınışı durumunda yeterince ayrıntılı değildir. Frege’nin geliştirdiği niceleme mantığı, tüm bu sorunları kökünden halletmiş ve modern mantığın gelişiminde yeni bir başlangıç olmuştur.
Frege’ çalışmasında, matematikte sınıf ve sınıfların sınıfları fikrini de geliştirmişti. Küme teorisini kullanarak belli bir sınıftan asal sayıları, benzeri türden tüm sınıfların sınıfı olarak tanımlamıştı.

Bertrand Russell ‘de kendisinin çalışmalarını yakından takip ediyordu. Ancak Frege’nin sembolik mantık üzerine temel bir çalışmasını incelerken garip bir durumu keşfetti. Bazı kümeler kendilerinin üyesidir, bazılarıysa değildir. Örneğin, felsefeciler kümesi kendisinin bir üyesi değildir çünkü bahsedilen şey bir filozoftur.
Ancak filozof olmayanlar kümesi kendisinin bir üyesidir. Dolayısıyla, kendilerinin üyesi olmadığı tüm kümelerin kümesi kendinin bir üyesi midir? Eğer öyleyse, demek ki değildir. Eğer değilse, demek ki öyledir. İşte Russell paradoksunun karşımıza çıktığı nokta da burasıdır.
Bizim açımızdan kavraması çok kolay olmasa da Gottlob Frege bu paradoksun önemini hemen kavrayacaktı. Bunun sonucunda da üzerinde 9 yıl boyunca çalışarak ulaştığı sonuçların temellerinin sarsıldığını anladı. ( Detaylar için: Akademik Dürüstlük ve Gottlob Frege’nin Hayal Kırıklığı)
Sonucunda Frege’nin matematiği mantığa indirgeme projesi başarısız oldu. Yine de Frege felsefi bir başarısızlıktan uzaktı. Geçtiğimiz yüzyılda, mantık, matematik ve dilin en önemli filozoflarından biri olduğunu kanıtladı.
Russel Paradoksu ile Küme Kavramına Yeni Bir Bakış Açısı Kazandırdı
Russell’ın paradoksuna bir dizi yanıt sunuldu. Bunlardan biri Russell’ın kendisi tarafından önerildi. Russell, Alfred North Whitehead (1861–1947) ile birlikte Principia Mathematica’da kapsamlı bir tipler sistemi geliştirdi. Bu sistem zahmetli paradokslardan kaçınmasına ve tüm matematiğin inşasına izin vermekteydi. Ancak hiçbir zaman geniş çapta kabul görmedi.
Bunun yerine, bugün kullanılan aksiyomatik küme teorisinin en yaygın versiyonu, tip kavramından kaçınan ve kümeler evrenini belirli aksiyomlar kullanılarak verilen kümelerden oluşturulabilecek kümelerle sınırlayan Zermelo-Fraenkel küme teorisi yaygınlaştı.
Bu kuram paradoksu ortadan kaldırmaktadır. Ancak bunun için de kuram içinde küme kavramı tanımsız bırakılmıştır. Bu nedenle temelde kümenin tanımını okuduğunuz her açıklama kusurludur. ( Detaylar için: Kümenin Tanımı Neden Yoktur?)

Sonuç olarak okuduğunuz bu paradoks, kümeler kuramının diğer paradoksları gibi bugün ortadan kalkmıştır. Russell Paradoksu ve modern aksiyomatik küme teorisindeki çözümü, matematik anlayışımızın zaman içinde nasıl geliştiğini gösterir.
Kaynaklar ve ileri okumalar:
- Russell’s Paradox: Here’s Why Math Can’t Have A Set Of Everything. Yayınlanma tarihi: 25 Kasım 2023; Bağlantı: https://www.businessinsider.com/
- Bertrand Russell’s Paradox Explained. Yayınlanma tarihi: 22 Kasım 2022; Bağlantı: https://www.thecollector.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel