Fiziksel dünyamızı Öklid uzayına uygun biçimde üç boyutlu olarak algılarız. Sonucunda algılarımıza uygun olan budur. Uzunluk, genişlik ve yükseklik biçiminde üç boyut vardır ve bir çoğumuza bu kadarı yeterlidir. Ancak pek çok problem sadece üç boyutlu uzay kullanılarak çözülemez. Bu yazımızda ele alacağımız Minkowski uzayında işin içine, dördüncü boyut olarak zaman eklenir.
Bu fikir Einstein’ın matematik öğretmenlerinden biri olan Hermann Minkowski tarafından 1909 yılında ortaya atılmıştır. Kendisi bize uzay ve zamanı tek bir formülde kavrayabileceğimizi göstermişti. Onun geliştirdiği uzay-zaman yani Minkowski uzayı tüm özel göreliliği tanımlar. Ayrıca kuantum alan teorisi hesaplamalarının büyük çoğunluğu için de bir zemin sağlar. Bu noktada elbette aşağıdaki soruyu sormakta haklısınız.

Minkowski Uzayı Tam Olarak Nedir?
Anlatmaya özel görelilik kuramından başlamalıyız. Einstein bunu 1905′ te dünyaya duyurduğunda denklemlere dayalı bir matematik kuramıydı. O sırada sandığınız kadar büyük bir yankı uyandırmadı. Aslına bakarsanız bilim camiasının oturup bunu fark etmesi birkaç yıl aldı. Bu da aslında Hermann Minkowski’nin 1908’de Cologne’da verdiği bir konferans sayesinde oldu.
Bu konferans sayesinde özel görelilik kuramının fikirleri uzay-zaman geometrisi cinsinden ilk gözler önüne serilmişti. Minkowski’nin özel görelilik kuramını muazzam biçimde basitleştirmesi büyük yankı uyandırmıştı. Einstein’ın Temmuz 1909’da Cenevre Üniversitesi’nden fahri doktora unvanını alması ve bir yıl sonrasında Fizikte ilk Nobel Ödülü’ne aday gösterilmesi tesadüf değildi.
Düzlemdeki yani iki boyutlu uzaydaki her nokta iki koordinatla ifade edilir. Aynı biçimde üç boyutlu uzaydaki her nokta üç koordinatla gösterilecektir. Buradan yola çıkarak dört boyutlu uzaydaki bir noktanın dört koordinat ile gösterilmesi gerekir.
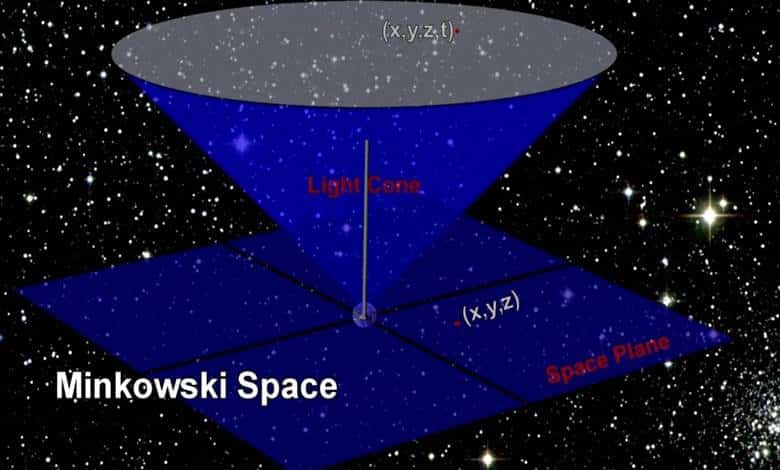
Minkowski diyagramı ya da uzay zaman diyagramı, Hermann Minkowski tarafından geliştirilen ve uzay ve zaman, Özel görelilik teorisi içinde yer alan uzay ve zamanın, özelliklerinin örneklerini temin etmeyi sağlayan diyagramdır. Aşağıda bunun bir örneğini görüyorsunuz.
Minkowski Uzayında Işık Konisi Ne Anlama Geliyor?
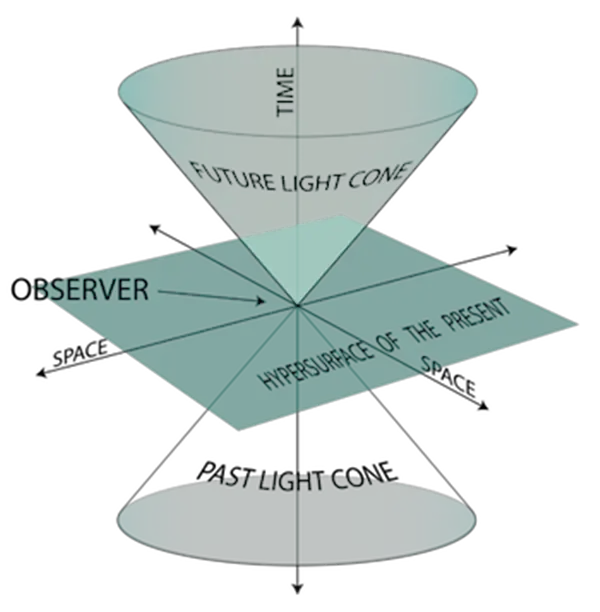
Bildiğiniz gibi Özel göreliliğin anahtar kavramlarından biri, zamanın göreceli olduğudur. Yani aynı olayı gözlemleyen iki kişi, göreceli hareketlerine bağlı olarak, farklı zamanlarda meydana geldiğini algılayacaktır. Öyleyse, zaman göreceliyse, yani her gözlemci için kişiselse, olayların ne zaman olduğuna nasıl karar verirsiniz? Evrendeki olayları nasıl sıralayacaksınız?
Bunu anlamak için uzay-zamandaki konumumuzda belirli bir A olayını gözlemlediğimizi hayal edeceğiz. Yukarıdaki görseli bir kere daha inceleyelim. Görselleştirmeyi kolaylaştırmak için, uzay-zamanın iki uzay ve bir zaman boyutu olmak üzere üç boyutlu olduğunu farz edeceğiz. Observer yani gözlemci ise biziz. Bir olay, düz bir düzlem üzerindeki bir noktadır. Bu düzlem ise belirli bir zamanda uzay-zamandaki bir dilimi temsil eder.
Görselde üstteki koni geleceği ve alttaki koni geçmişi simgeliyor. Yani üst taraf A olayının gelecekteki ışık konisi olarak adlandırılan şeydir. Bu koni, A olayından etkilenebilecek tüm olayları içerir. Benzer şekilde, geçmiş ışık konisi, uzay-zamanda bir sinyal gönderebilen, en fazla ışık hızında hareket eden ve A olayına ulaşabilen tüm olaylar olarak tanımlanır. Kısacası bu diyagram aracılığıyla geçmiş ve gelecek ışık hızına göre belirlenir ve sıralanır.
Yukarıda tanıttığımız ışık konisi yapısı bu geometrinin önemli bir unsurudur. Ancak Minkowski geometrisi deyince bundan daha fazlası anlaşılmalıdır.
Minkowski uzayı ve Öklid uzayı arasındaki fark nedir?
Öklid geometrisinde iki nokta arasındaki mesafe bir değişmezi ifade eder. Koordinat sistemi değişse dahi yer değiştirme sabit kalır. Ayrıca bildiğimiz gibi mesafe her zaman pozitif olmalıdır. Sıfır olduğu durum ise hareketin olmadığı durumu ifade eder.
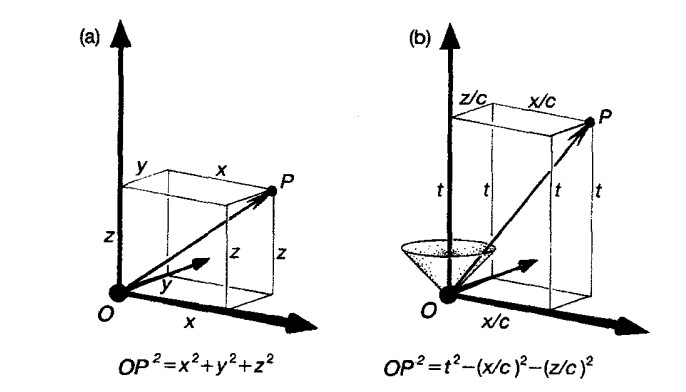
Minkowski geometrisinde de bu duruma benzerlikler taşıyan bir uzaklık kavramı vardır. Üç boyutlu Öklid geometrisinde, bir noktanın merkeze olan r uzaklığı ise aşağıdaki bağlantıyı yazmamız olasıdır. İki boyutlu durumda ise bu ifade aslında hepimizin bildiği Pisagor teoremine dönüşecektir.
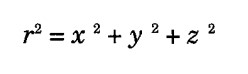
Minkowski geometrisinde de, esas olarak aynı şeyi kullanırız. Temelinde fark tek bir işarettir. Sonucunda dört boyutlu Minkowski geometrisini dikkate aldığımız da ‘uzaklık’ ifadesi şöyledir. Ancak uzaklık bu durumda geçen zaman anlamındadır.
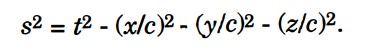
(t, x / c, y / c, z / c) koordinatlarına sahip P noktasının, üç boyutlu uzayda O olayının (gelecek) ışık konisinde yer aldığını varsayalım. Minkowski uzayında, OP doğru parçasının s uzunluğu, O ve P olayları arasında geçen zamandır.
Görseldeki ‘t’, yalnız gözlemciler için geçen zamanı bildirir. Hareketli (0 merkezinden sabit hızla uzaklaşan) bir gözlemci için ‘doğru’ süre ölçümü, özel göreliliğe göre, s niceliği tarafından sağlanır.
Yukarıdaki formüle göre, x / c, y / c, z / c değerlerinin tümü sıfır olmadığı sürece s2, t2‘den küçüktür. Bu durum zamansaldır. Yani iki olayın aynı yerde meydana geldiği ancak aynı anda gerçekleşmediği bir referans çerçevesi olduğu anlamına gelir.
Öte yandan hız, ışık hızına eşitse, bu durumda P ışık konisi üstünde yer alır ve s= 0 buluruz. Metriğin sıfırlanmasını sağlayan eleman ve olaylar ışıksaldır. Minkowski uzaklığı sıfır ise, biri ötekinin ışık konisinde yer alan iki nokta elde ederiz ve böylece o noktadaki ışık konisini tanımlarız. Ancak s2‘nin, t2‘den büyük olduğu durumlarda maddesel parçacıkların veya fotonların ışıktan daha hızlı hareket edemeyeceklerine dair kuralı çiğnemiş oluruz. Bu durumda da olaylar uzaysaldır.
Sonuç olarak;
Bu yazımız sadece konuyu özetlemek adına yazılmıştır. Ancak sonuç olarak gördüğünüz gibi Minkowski uzayının ana yapısı, özel göreliliğin özünü içerir. Bu gösterimde, özel göreliliğin gerektirdiği fiziksel harekete ilişkin her olgu uzay-zamanın geometrisine ilişkin bir teorem olarak ifade edilmektedir.
Konu ile ilgili aktarılacak çok fazla şey olsa da hepsini bir yazıda toparlamamız olası olmayacaktır. Bu nedenle eğer ilginizi çektiyse bizim de bu yazı esnasında faydalandığımız Roger Penrose tarafından kaleme alınan Fiziğin Gizemi isimli kitabı edinmenizi ve okumanızı öneririz.
Kaynaklar ve İleri okumalar:
- Violating causality. Yayınlanma tarihi: 15 Ağustos 2017; Bağlantı: https://plus.maths.org
- Ask Ethan: What Is Spacetime? Yayınlanma tarihi: 28 Ocak 2017; Bağlantı: https://www.forbes.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel