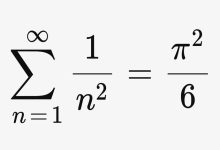Hepimiz çarpma işleminin nasıl yapıldığını biliyoruz. Diyelim ki sizden 691 ile 389’u çarpmanız istendi. Siz de çoğu insan gibiyseniz, muhtemelen cevabı telefonunuzun hesap makinesi ile hesaplarsınız. Ancak çaresiz kalırsanız ilkokulda öğrendiğiniz aşağıda gördüğünüz yöntemi uygularsanız.
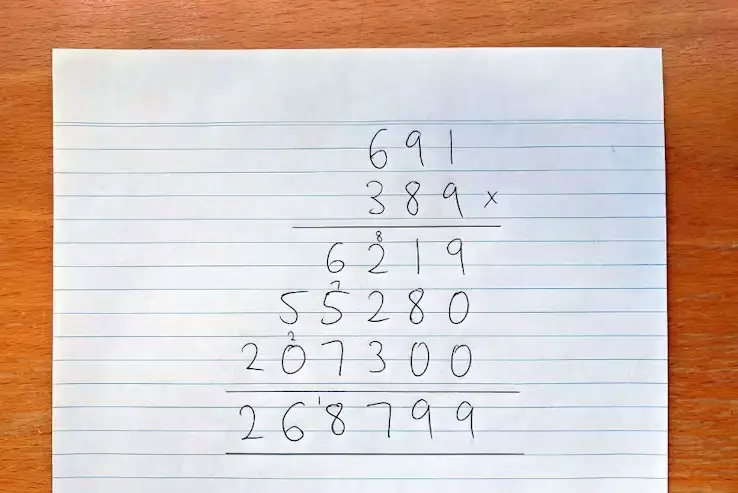
İlköğretim yıllarının başında öğrendiğimiz bu yöntem de elbette sorun yoktur. Hatta küçük sayıları birbiri ile çarpmak için en kolay metot elbette hala budur. Bu yöntemde alttaki sayının her basamağını tek tek üstteki sayı ile çarparız. Sonrasında da çıkan sonuçları toplarız. Bu durumda iki sayının her biri N rakama sahipse, bu toplam N 2 (veya N x N ) çarpım yapmamız gerekecektir.
Yukarıdaki örnekte sayılarımız üç basamaklıdır. Bu nedenle de 3 2 = 9 çarpma işlemi yaparak sonucu elde etmemiz mümkün olmuştur. Bu durumda 100 basamaklı iki sayıyı çarpmak için 10000 adet çarpma işlemi yapmak gerekir. Bilgisayarlar bile sayılar büyüdükçe uzun çarpma işlemi ile ilgili sorunlar yaşamaya başlarlar. Bir milyar basamaklı iki sayıyı çarpmak, 1018 tane çarpma gerekir. Bu da modern bir bilgisayarın yaklaşık 30 yılını alır.
Peki bu gerçekten iki büyük sayıyı çarpmanın en iyi yolu mu? 1956 civarında ünlü Sovyet matematikçi Andrey Kolmogorov, iki sayıyı çarpmanın mümkün olan en iyi yolunun bu olduğunu tahmin etti. Kolmogorov, eğer daha kısa bir yol mümkün olsaydı kesinlikle keşfedilmiş olacağını düşünüyordu. Ancak bir kaç yıl sonra yanıldığını anlayacaktı.
Karatsuba Yöntemi İle Çarpma İşlemi Nasıl Yapılır?
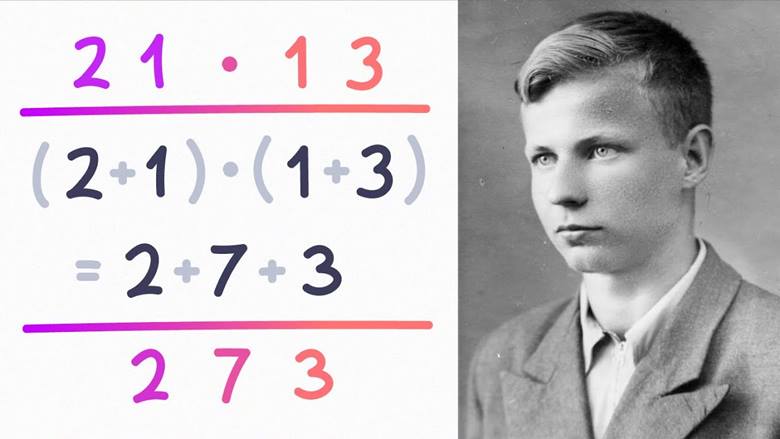
1960 yılında, Rus matematikçi Anatoly Karatsuba, çarpmanın daha verimli bir yolunu bulmak için yola koyuldu ve sonunda yeni bir üst sınır buldu. Karatsuba, ‘ AB ‘ ve ‘ CD iki basamaklı sayılarının çarpımını hesaplamak için gereken dört küçük çarpmanın hepsinin , A + B ve C + D rakamlarının toplamlarını çarptığımızda da ortaya çıktığını fark etti. Bunun nasıl yapıldığını anlamak için aşağıdaki görseli incelemenizi öneririz.
Karatsuba tekniği kesinlikle küçük sayıları çarparken kullanacağınız bir yöntem değil. Ancak daha verimli bir yöntem. Örneğin, 1.234 ve 5.678 gibi dört basamaklı iki sayıyı çarpmak istediğimizi varsayalım. Geleneksel çarpma teknikleri, toplam 4 × 4 = 16 küçük çarpma işlemi gerektirecektir. Ancak Karatsuba’nın yöntemini kullanarak bunu 9 küçük çarpma işlemine indirmeniz mümkündür.
Bu fazla önemli bir avantaj gibi gelmemiş olacaktır. Ancak rakamlar büyüdükçe avantajı anlamaya başlarsınız. Bin basamaklı sayılar için Karatsuba’nın yöntemi, uzun çarpmaya göre yaklaşık 17 kat daha az çarpma işlemine ihtiyaç duyuyor.
Peki “neden birileri bu kadar büyük sayıları birbiriyle çarpmak istesin ki?” diye düşünüyor da olabilirsiniz. Cevap elbette güvenlik olacaktır. İnternette her şifreli iletişim kurduğunuzda, cihazınız yüzlerce hatta binlerce basamaklı sayıları çarpmak zorundadır. Büyük olasılıkla cihazınız bu işlem için de Karatsuba çarpmasını kullanacaktır. Bunların hepsi, web sayfalarımızın mümkün olduğunca çabuk yüklenmesini sağlayan muhteşem yazılım ekosisteminin bir parçasıdır.
Çarpma İşlemini Daha Hızlı Yapmak İçin Uzun Yıllardır Yeni Yöntemler Araştırıyoruz
Bir bahşişi hesaplarken Karatsuba çarpmasını kullanmazsınız, ancak iş büyük sayıları çarpmaya geldiğinde, onu yöntemi büyük bir ilerlemeydi. Ve Karatsuba 1960’ta daha hızlı çarpmanın kapısını açtığından beri matematikçiler, Fourier dönüşümü gibi gelişmiş teknikleri kullanarak yeni hız rekorları kırıyorlar.
Çünkü bazı uygulamalar için matematikçiler milyonlarca, milyarlarca ve hatta trilyonlarca rakamdan oluşan daha da büyük sayılarla uğraşmak zorundadır. Bu kadar muazzam sayılar için Karatsuba’nın algoritması bile çok yavaş kalacaktır.

Aslına bakarsanız Karatsuba algoritmasının hükümdarlığı, Arnold Schönhage ve Volker Strassen’in 1971 de yayınladıkları bir makale ile son buldu. İki Alman matematikçi tarafından geliştirilen Schönhage-Strassen algoritması aslında 1971’den 2007’ye kadar en hızlı çarpma yöntemiydi. Yöntemleri bugün matematikçiler tarafından milyarlarca basamaklı sayıları çarpmak için rutin olarak kullanılıyor. Ancak daha hızlısının da mümkün olduğu kısa zaman sonrasında anlaşılacaktı.
Yazının bu noktasında kısa bir teknik bilgi vermemiz gerekecek. İkili geliştirdikleri yöntem ile N basamaklı sayıları en fazla N log (N) ile orantılı bir dizi temel işlem kullanarak çarpmanın mümkün olması gerektiğini bizlere göstermişti. Ancak kendi bu hedefe tam olarak ulaşamamıştı.
1971’den bu yana geçen on yıllarda, birkaç araştırmacı Schönhage ve Strassen’in algoritmasında iyileştirmeler yaptı. Hatta Martin Fürer tarafından 2007’de tasarlanan bir algoritma, N log (N) sınırına oldukça yaklaştı. Bu süreçte de kimi matematikçiler N log (N)’in gerçek bir sınır olup olmadığını, daha hızlı çarpma algoritmaları geliştirmenin mümkün olup olmadığını sorgulamaya başladılar.
Çarpma İşlemi İçin Bir Sınıra Ulaştık mı?
Cevap hayır gibi gözüküyor. Yakın zamanda David Harvey ve Joris van der Hoeven adlı matematikçiler, çarpma işlemini daha hızlı yapmak için farklı bir yöntem önerdi. Bu yöntem sayesinde çok büyük sayıları çarpmak artık çok daha kısa sürüyor.
Yeni algoritma şu anki haliyle pek pratik değil çünkü kanıt yalnızca çok büyük sayılar için işe yarıyor. Öte yandan, daha fazla iyileştirmeyle algoritmanın kullanışlı hale gelebileceği düşünülüyor. Schönhage-Strassen varsayımı doğruysa, bu yeni algoritma yolun sonu anlamına da geliyor.
Bu durumda şimdilik çarpma işlemini yapmak ile ilgili en hızlı yolu bulmuş durumdayız. Ancak unutmayın. Bu hız, biz insanlar için değil temelinde bilgisayarlar için gereklidir. Bu nedenle siz nasıl biliyorsanız aynı biçimde çarpma yapmaya devam edebilirsiniz. Ayrıca çarpma yapmanın eğlenceli bir yoluna da göz atmak isterseniz: Çarpma Yapmanın Eğlenceli İki Yolu: Rus Çiftçi Ve Antik Mısır Çarpımı
Kaynaklar ve İleri Okuma:
- Mathematicians Discover the Perfect Way to Multiply. Yayınlanma tarihi: 11 Nisan 2019; Kaynak site: Quanta Magazine. Bağlantı: Mathematicians Discover the Perfect Way to Multiply/
- This Guy Just Found a Faster Way to Multiply. Yayınlanma tarihi: 19 Ekim 2019. Kaynak site: Popular Mechanics. Bağlantı: This Guy Just Found a Faster Way to Multiply/
- On Your Mark, Get Set, Multiply. Yayınlanma tarihi: 23 Eylül 2019. Kaynak site: Quanta Magazine. Bağlantı: On Your Mark, Get Set, Multiply/
- Schönhage, A., Strassen, V. Schnelle Multiplikation großer Zahlen. Computing 7, 281–292 (1971). https://doi.org/10.1007/BF02242355
- Fürer, Martin. (2009). Faster Integer Multiplication. Proceedings of the Annual ACM Symposium on Theory of Computing. 39. 10.1137/070711761.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel