Matematiksel bilmeceler tarihin en parlak zihinlerini bile her zaman büyülemiştir. Günümüzde de bu popülerliğin korumasında Martin Gardner’ın çalışmaları önemlidir. “Bulmacalar sizi matematiğin hemen hemen her dalına götürebilir.” diyen Martin Gardner bir matematikçi olmamasına rağmen matematiğe ilgi duyulmasına sağladığı katkılardan dolayı matematikçiler arasında anılmayı hak eder.
Martin Gardner hayatının çoğunu gazeteciliğe ve genel olarak bilimin halka yaygınlaştırmaya adamıştır. Gardner, 1978’de Bucknell Üniversitesi’nden fahri doktora ve 1983’te Amerikan Fizik Enstitüsü’nün yılın bilim yazarı ödülü de dahil olmak üzere kayda değer katkılarından dolayı bir dizi onursal ödül almıştır.

Gardner’in amacı sadece soruları çözdürmek değil, okurlara doğru cevabı aratarak biraz zihinleri bulandırmaktı, bunda da başarılı olduğu şüphesiz.. Bu yazıda da o kitaplardan alınan sekiz bulmaca bulunmakta.
“Kesinlikle bir öğrenciyi uyandırmanın en iyi yolu bulmaca, sihirbazlık numarası, şaka, paradoks gibi ilginç bir matematik oyunları ile onun ilgisini çekmektir ancak bu şeylerden önemsiz gibi görünmeleri nedeniyle öğretmenler kaçma eğilimindedir”
Martin Gardner
Martin Gardner Bulmacaları
1- Çılgın Kesik: Bir kesik yaparak ya da çizgi çizerek bu şekli iki özdeş parçaya bölünüz.

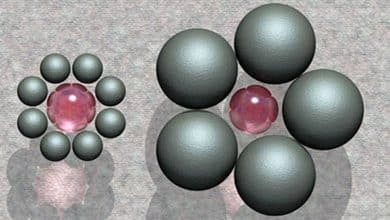
2- Renkli Çoraplar: On kırmızı ve on mavi çorap bir tuvalet çekmecesinde karıştırılıyor. 20 çorap da renkleri hariç birbirlerine benziyor. Oda karanlık ve çorapları ikişerli eşleştirmek istiyorsun. Eşleşen bir çifti bulduğuna emin olmak için çekmeceden çıkarman gereken en az çorap sayısı kaçtır?
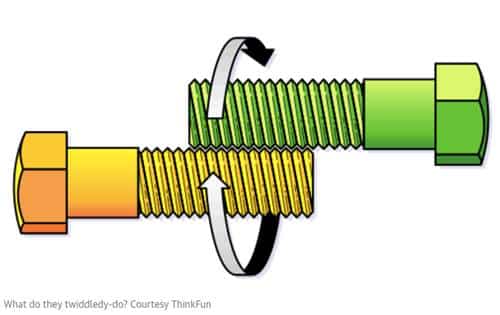
3- Çift Cıvatalar: İki özdeş cıvata, sarmal olukları birbirine geçecek şekilde yerleştirilir. Cıvataları, birbiri etrafında gösterilen yönde hareket ettirirsen; kafaları: (a) içe doğru mu hareket ederler, (b) dışa doğru mu hareket ederler veya (c) birbirlerine aynı mesafede mi kalırlar?
4- Yolda Çatallanma: Bir mantıkçı tropik bir adada planladığı tatilinde, kendisini iki kabilelerinin yaşadığı bir adada bulur. Bir kabilenin üyeleri her zaman gerçeği söylemektedir, diğer kabilenin üyeleri ise her zaman yalan söylemektedir. Mantıkçı bir yol ayrımına gelir. Yerli halktan birine hangi yolun kendisini köye ulaştıracağını sorması gerekmektedir. Bu kişinin gerçeği mi yoksa yalan mı söyleyen biri olduğunu anlamak için bir soru sorar. Cevaptan hangi yolu seçeceğini bilir. Sorduğu soru nedir?
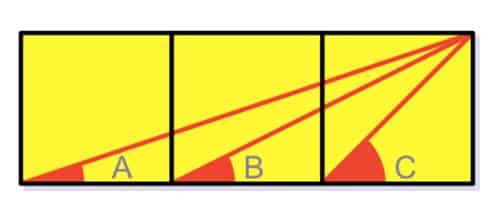
5- Üç Kare: Yalnızca temel geometri (trigonometri bile değil) kullanarak, C açısının A ve B açılarının toplamına eşit olduğunu kanıtlayın.
6- Pastayı Kesmek: Düz bir kesikle bir pastayı iki parçaya bölebilirsiniz. Birinci kesiği kesen ikinci bir kesik dört parça meydana getirecektir ve üçüncü bir kesik ile en çok yedi parçaya kadar parça elde edilebilir. Altı düz kesikle elde edebileceğin en fazla parça sayısı nedir?
7- Parçalanmış Satranç Tahtası: Bu soru için gerekenler bir satranç tahtası ve 32 domino taşı. Her bir domino, satranç tahtasındaki iki kareyi tam olarak kapsayacak büyüklüktedir. Bu yüzden 32 domino satranç tahtasındaki 64 karenin tamamını kaplayabilir. Ama şimdi tahtanın karşıt köşelerindeki iki kareyi kestiğimizi ve domino taşlarından birini çıkardığımızı varsayalım .Geriye kalan 62 karenin tamamen kaplanabilmesi için 31 domino taşını tahtaya yerleştirmek mümkün müdür?
Bulmacaların çözümleri
1- Çizgi düz olmak zorunda değildi.

2- Üç çorap çıkardığında her zaman eşleşen bir çift vardır.
3- Çözüm: (c). Sarmal oluklu cıvataların kafaları ne içe ne de dışa doğru hareket eder. Hareketleri birbirlerini etkisiz hâle getirir.
4- Yol ayrımından birini işaret edin ve yerliye sorun. “Eğer sana bu yolun köye gittiğini sorsaydım, bana evet der miydin?” Eğer yol doğru olansa, bir yalancı bu soruya hayır cevabını verecektir. Bu durumda yolunuz doğrudur.
Eğer yol doğruysa gerçeği söyleyen de yine evet diyecektir. (Çevirmen Notu: Gösterilen yol yanlış yolsa, sorulan asıl sorunun soruluş şeklinden dolayı yalancı hayır diyecektir; gerçeği söyleyen zaten hayır diyecektir. Yani her iki durumda da gösterdiğimiz yolun doğru olan mı yoksa yanlış olan mı olduğunu öğreniyoruz.)
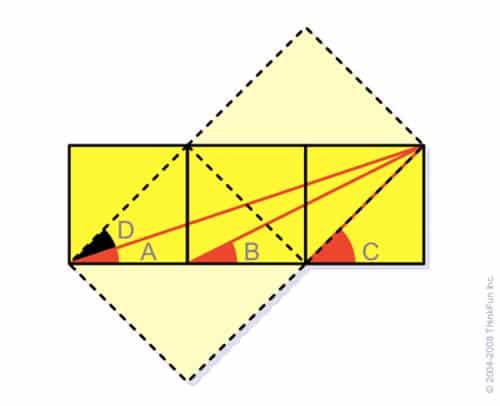
5- İşte bunu yapmanın bir yolu. Kesikli çizgilerle gösterilen ek kareleri oluşturun. B ve D açılarının ikisi de, bulundukları üçgenlerde dik kısa kenarı gösterir. Bu yüzden üçgenlerde benzerlikten yöndeştirler ve dolayısıyla eşittirler.) Bu nedenle A ile D toplamında D yerine B yazabiliriz; bu da C açısının A ile B açılarının toplamına eşit olduğunu gösterir.
6- İlk kesik pastayı 2 parçaya böler. İkinci kesik 2 parça daha getirir ve toplam parça 4’e çıkar. Üçüncü kesik toplamı 7’ye çıkartan 3 parça daha getiriyor. Her kesik, kaçıncı kesik sayısı olduğuna göre toplam parça sayısına parça ekliyor gibi gözüküyor. Böylece, dördüncü kesik en çok 4 yeni parça, beşinci kesik en çok 5 yeni parça ve altıncı kesik en çok 6 yeni parça oluşturacaktır. Dolayısıyla oluşacak en fazla parça sayısı 22’dir.
7- Bu satranç tahtası, 31 domino taşıyla kaplanamaz. Detaylı bir çözüm için bu yazımızı inceleyiniz. Düşündürücü İki Basit Satranç Tahtası Problemi
Konuk Yazar: Atakan Yücel
Matematiksel