Bu yazı bir uyarıyla birlikte gelir. Bu soruyu çözmeye uğraşmayınız. Başlangıçta sorunun basitliği, kolayca anlaşılabilir olması size cazip gelecektir. Hemen elinize kağıt kalem alıp denemek bile isteyebilirsiniz. Ancak hatırlatalım. Kimileri için “3n+1 problemi” kimileri için de onu gündeme taşıyan Lothar Collatz’a atfen Collatz Problemi ya da Collatz Sanısı olarak bilinen bu problem ile matematikçiler 1970 yılından beri uğraşıyorlar.
Collatz Problemi Nedir?
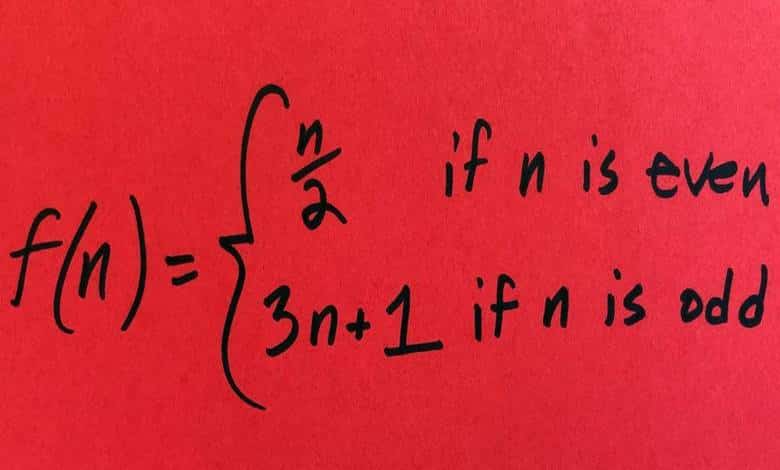
1932’de, 20 yaşında bir Alman matematik öğrencisi olan Lothar Collatz, ilk bakışta basit bir hesaplamadan başka bir şey gibi görünmeyen bir muamma ile karşılaştı. Kural çok basitti. Herhangi bir sayı seçin. Eğer sayınız çift ise 2’ye bölün, tek ise 3 ile çarpıp 1 ekleyin. Sonra, sonucunuza yine aynı kuralı uygulayın. Bu işlemi istediğiniz kadar tekrar edin.
Göreceksiniz ki hangi sayıyla başlarsanız başlayın sayılar eninde sonunda 4, 2, 1, 4 … döngüsüyle devam edecek. Örneğin n=5 için 5, 16, 8, 4, 2, 1, 4, 2, 1 şeklinde olacaktır. Benzer biçimde n=11 için, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1. Aşağıdaki örneklerde diğer sayılar için alacağı sonuçları da görebilirsiniz.

Collatz Problemi Aslında Bir Çok Farklı İsimde Karşımıza Çıkar
Başta da dediğimiz gibi Collatz varsayımı şaşırtıcı derecede basit olması nedeniyle kışkırtıcıdır. Aynı zamanda da basitliği yanıltıcıdır. Şu ana kadar denediğimiz her sayı aynı döngüye girse de bunun her zaman doğru olup olmadığından emin değiliz. Zaten bu nedenle de kendisinden aslında bir varsayım olarak bahsediyoruz.

Lothar Collatz başta da dediğimiz gibi bu döngüyü ilk fark eden kişiydi. Ancak kendisi ne varsayımını kanıtlamayı ne de bir karşı örnek bulmayı başardı. Collatz hayatı boyunca bu varsayım hakkında kayda değer bir şey yayınlayamadı. Collatz Problemi, 2. Dünya Savaşı sırasında bir süre Polonyalı matematikçi Stanislaw Ulam tarafından ele alındı. Boş zamanlarında Ulam, varsayımı araştırdı, ancak bir kanıt bulamadı. Bu problem bu nedenle bir süre Ulam’ın ismi ile anıldı.

Devamında Hamburg Üniversitesi’nden sayısal bir kuramcı olan Helmut Hasse bu tuhaf bulmacanın ile uğraşmaya başladı. Almanya’da ve yurtdışında konu ile ilgili konferanslar verdi. Bu konferanslar esnasında bu sayılar bir dinleyici tarafından dolu tanelerine benzetildi. Bu sebeple bir süre bu problemin adı “Dolu Tanesi Sayıları” diğer adıyla Hailstone dizisi olarak anılmaya başlandı.
Sonrasında Japon matematikçi Shizuo Kakutani konuyla ilgili konferanslar verdi. Problem bu esnada da Kakutani problemi olarak bilinmeye başlandı. Bu arada işin içine bilgisayar karıştı. Süper bilgisayarların yardımıyla bugüne kadar, matematikçiler yaklaşık 300 kentilyon sayıyı denediler. Hepsinin varsayımına uyduğunu gördüler! Bu yeterli mi? Hayır değil! Sonsuza kadar tüm sayıları kapsayacak şekilde herhangi bir pozitif tamsayı “n” için bir kanıt yazamadığınız sürece, bu varsayımı bir teoreme çeviremezsiniz!
Collatz Problemini Çözmek Mümkün mü?
Bu varsayımı grafik çizimlerle kanıtlamak için çeşitli girişimlerde bulunuldu. Sonucunda yapılması gereken sırasıyla bütün başlangıç sayılarını düşünmek yerine uygun bir model oluşturmaktı. Ancak sorun karşımızda bazen bir düzen, bazen de bir düzensizliğin var olmasıdır. Kesinlikle rastgele değildir; ama kalıp olarak yazılması da mümkün değildir.
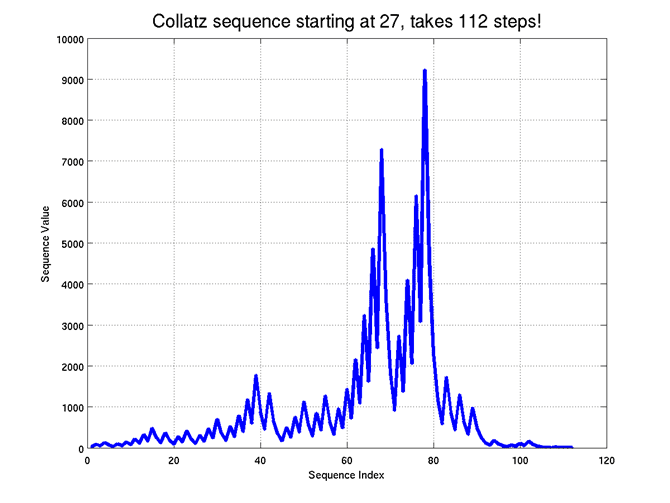
İlk 50 sayı içerisinde 1 sayısına geri dönmek için en uzun yol alan sayı 27’dir. Tam 112 adım. Şekilde görüldüğü gibi, 67. adımda 7288, 77. adımda 9232 yüksekliğine çıkar ama sonra birden çöküşe geçer ve bir kaç çırpınışın ardından 1 sayısına geri döner.
Bu sayılar arasında bir kaç rekortmen sayı da vardır. Mesela 703 başlangıç sayısı olarak alınırsa, dizi 170 adım sürer ve zirveye 250 504 sayısında zirve yapar. Bir diğer rekortmen ise 26 623 başlangıç sayısıdır. Bu sayıda tam 307 adım sürer ve zirveye 10 358 020 sayısında ulaşır. Ancak zirveye ulaştıktan sonra kaçınılmaz sonları 1 sayısına geri dönmek olacaktır.
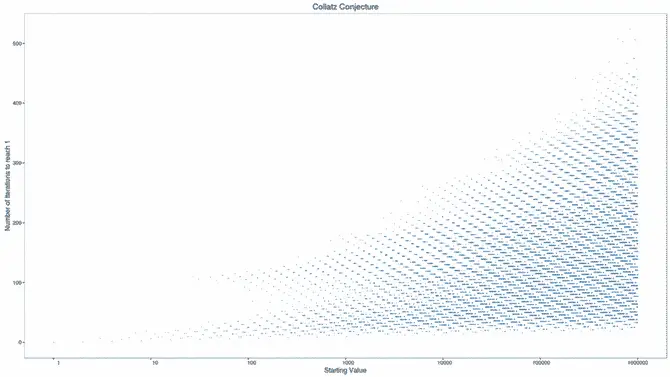
Bir hesap makinesi desteği ile 1 den 100’e kadar olanları sizde listeleyerek bu ilginç dağılımları görebilirsiniz. Çok fazla sürer diye düşünmeyin. Örneğin 7 sayısını ele alalım. 7,22,11,34,17,52,26,13,40,20,10,16,8,4,2,1….
Bu dizi bize sadece uzunluğun 16 ve zirve değerinin 52 olduğunu söylemiyor. Aynı zamanda 22 olan ikinci sayı içinde uzunluğun 16, zirve değerinin 52 olduğunu, üçüncü olan 11 içinde uzunluğun 14 zirve değerinin 52 olduğunu söylüyor. Bu biçimde düşünürsek zaten bir tek sayı bize 16 tane sayı hakkında zaten bilgi vermekte…
Collatz Problemi Çözümsüz Olabilir mi?
Paul Erdös bu sayılar ile ilgili yorumunda, “Matematik henüz böyle problemlere hazır değil “demişti. Yine de bu uyarı yıllardır matematikçileri bu probleme bir cevap aramaktan alıkoymuyor. 2019’da dünyanın yaşayan en büyük matematikçilerinden biri olan Terence Tao problemin çözümü için önemli bir atılım yaptı. Bu sayede Collatz varsayımı “neredeyse” tüm sayılar için “neredeyse” doğru olarak tanımlanmaya başladı.
Ancak elbette bu cevap sizin de fark etmiş olduğunuz gibi tam olarak elde etmeyi amaçladığımız bir cevap değildir. Dikkat etmiş olacağınız gibi varsayımın tam bir kanıtını sunamasa da bu bir ilerlemeydi. Sonucunda Collatz problemi hala çözümsüz. Ayrıca bu varsayımının hiçbir zaman doğru ya da yanlış olduğunu kanıtlayamamamız da mümkündür.
Ancak yine de şu anda bir yerlerde yüzlerce kişi bu probleme kafa yormaya devam ediyor. Belki de siz de onlardan birisinizdir. Esasen matematiğin güzelliği de zaten budur. Yine de hatırlatalım. 268‘den küçük her sayı için bu problem doğrulanmıştır. Dolayısıyla, bir karşı örnek arıyorsanız, yaklaşık 300 kentilyondan başlamalısınız. Bu nedenle denemek isteyenlere şimdiden sabırlar diliyoruz. Yazının devamında göz atmanızı öneririz: Bugüne Kadar Çözülmüş En Zor 9 Matematik Problemi
Kaynaklar ve ileri okumalar:
- The Simplest Math Problem No One Can Solve – Collatz Conjecture. Bağlantı: https://www.youtube.com/watch?v=094y1Z2wpJg
- The Simple Math Problem We Still Can’t Solve; yayınlanma tarihi: 23 Eylül 2020; Bağlantı: https://www.quantamagazine.org/
- Mathematician Proves Huge Result on ‘Dangerous’ Problem; yayınlanma tarihi:11 Aralık 2019; Bağlantı: https://www.quantamagazine.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel