Bir bisiklet tekerleğinin kenarına küçük bir ışık taktığınızı hayal edin. Şimdi uzaktan bir yerden, bisikletin hareketi esnasında nasıl bir şekil ortaya çıktığına bakın. Göreceğiniz şey aşağıdaki görseldekine benzeyecektir. Bir doğru boyunca dönerek ilerleyen bir çemberin üzerindeki sabit bir noktanın takip ettiği yola sikloid eğrisi denir

Sikloidler, son 500 yılda birçok önde gelen bir çok matematikçi tarafından incelenmiştir. Ayrıca matematikçiler arasında pek çok tartışmaya da neden olmuştur. Tartışmalardan biri şekli kimin keşfettiğiyle ilgili. Adı geçen en eski aday, Pisagor’un biyografisini yazan Iamblichus’tur (MS 245 – MS 325 civarı). Adı geçen diğer kişiler arasında Alman Cusalı Nicholas (1401-1464), Fransız Charles de Bovelles (1475-1566), İtalyan Galileo Galilei (1564-1642) ve Fransız Marin Mersenne (1588-1648) gibi çok sayıda kişi vardır.
Bir çok kaynakta itibarı Galileo almış gibi gözükse de matematik camiası hala ilkin kim olduğu konusunda anlaşamamaktadır. Ancak sikloid eğrisini detaylaı olarak inceleyen ve aslında eğriye adını veren kişi Galileo olduğu için itibarı onun kazanması da haksız bir sonuç sayılmamaktadır. Ayrıca kendisinin sikloid eğrisinin altındaki alanı anlamak amacıyla metal levhadan sikloid modelleri inşa edecek kadar ileri gittiği de bilinmektedir.

Zamanla sikloidler diğer ünlü matematikçilerin de ilgisini çekecekti. Sikloid üzerine kalıcı çalışmalar yapan bir diğer kişi de Blaise Pascal (1623–1662) idi. Pascal’ın bir gece diş ağrısından uyuyamayınca sikloid eğrisiyle uğraşırsa ağrısını unutacağını düşünüp masasının başına geçtiği rivayet edilmektedir. Sonucunda sikloidlerin özelliklerini düşünerek diş ağrısından kurtulmuş ve bunu bir işaret olarak kabul ederek matematiksel araştırmalarına devam etmiştir.
Sikloid Eğrisi Neden İlginç Bir Eğridir?
Pascal, sikloidle ilgili bazı problemler önermişti. Hatta sikloidin (1) ağırlık merkezini, (2) alanını ve (3) hacmini hesaplamak için bir yarışma bile düzenledi. Anlaşılan bu yarışmayı kimse kazanmamıştı. Ancak Londra’daki St. Paul Katedrali’nin ünlü tasarımcısı Christopher Wren (1632–1723), yarışma sorularından biri olmasa da, bir sikloid yayının uzunluğunun, onu oluşturan çember ile ilişkisi olduğunu kanıtlayacaktı.
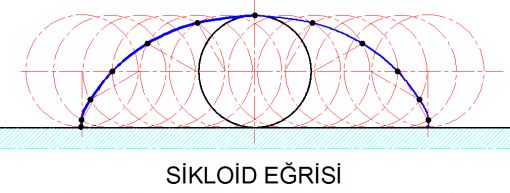
Sikloid eğrisi gerçekten de ilginç bir eğridir. Uzaktan baktığınız zaman gördüğünüz şekli bir çember yayına benzetmiş olmanız olasıdır. Ancak bu eğrinin denklemlerini çıkarmaya çalışınca bunun bir çember yayı olmadığını görürsünüz. Gerçekten de bir çemberin tam dönüşüyle elde edilen sikloid eğrisinin uzunluğu onu çizen çemberin çapının dört katı, altında kalan alan ise onu çizen çemberin alanının üç katıdır. Bugün bunu integral hesabıyla göstermek kolaydır. Ancak 1658’de bu müthiş bir başarıydı.
Sikloid Eğrisi Brachistokron Probleminin de Cevabıdır
1696’da Johann Bernoulli, brachistokron – veya en kısa zaman – problemi olarak adlandırdığı bir problemi ortaya atmıştı. Bu problem, dönemin matematikçilerine için açık bir meydan okumaydı. Daha da önemlisi, Johann Bernoulli’nin dünyaya ne kadar büyük bir matematikçi olduğunu göstermesi için bir şanstı. Genç Bernoulli dik bir düzlemde, iki nokta arasındaki mesafenin en kısa sürede alınmasını sağlayacak yolun şeklinin ne olması gerektiğini soruyordu. Ancak hareketin sadece yerçekimi etkisiyle ve sürtünmesiz bir ortamda gerçekleşmesi gerekiyordu.
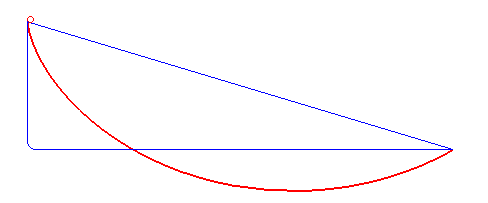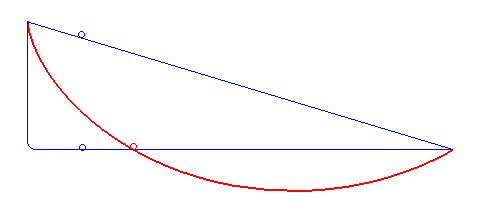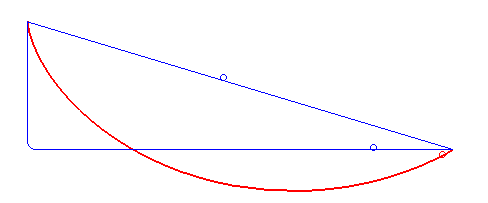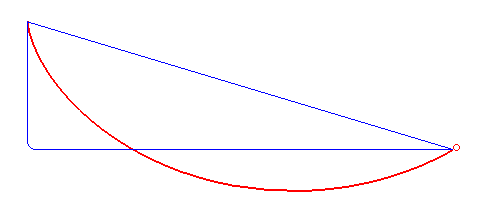
Yanıt veren beş matematikçi arasında Newton, Leibniz ve Johann’ın erkek kardeşi Jakob da vardı. Bir çok matematikçi soruyu çözmüş olsa da, Bernoulli’nin çözümü benzersiz, zekice ve şaşırtıcı derecede basitti. İstenen yol ise yine bir sikloid eğrisi idi. ( Daha fazlası için: Brakistokron Problemi: En Kısa Yol En Hızlı Yol Değildir!)
Sikloid ailesinin bir başka üyesi de Yunanca’da “aynı zaman” anlamına gelen tautochrone eğrisidir. Bu eğrinin herhangi bir yerine bir bilye yerleştirebilirsiniz, tüm bilyelerin aşağıya yuvarlanması aynı süreyi alacaktır.
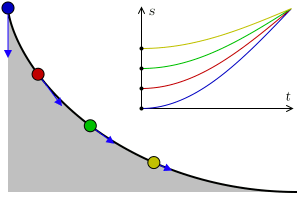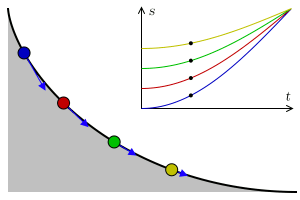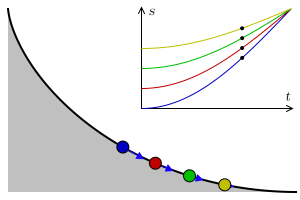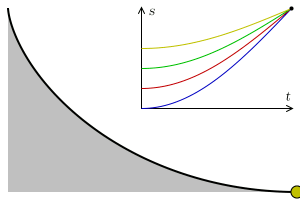
Sikloid Eğrisi Ne İşe Yarar?
Sikloidler şıklıklarının yanı sıra faydalı mıdır? Doğanın herhangi bir yerinde görünüyorlar mı? Bazı geometrik akrabalarının seviyesine ulaşamasa da, sikloidler doğal dünyada bazı şaşırtıcı yerlerde karşımıza çıkacaktır. Örneğin lunaparklarda hız trenlerinin en çok heyecan uyandıran iniş raylarında sikloid eğrisi kullanılır. Ayrıca sikloid eğrisi ve burada sözünü etmediğimiz pek çok eğri bugün gerek mimaride yapılara biçim ve güç katmakta gerekse otomotiv endüstrisinde en az sürtünmeyle çalışan dişlilerin yapımında kullanılmaktadır.

Muhtemelen siz de çocukken sikloidlerle oynamışsınızdır. Hasbro’nun 1960’ların ortasından beri üretilen Spirograph oyuncağı, hiposikloid adı verilen sikloidlerin değiştirilmiş bir formuna dayanmaktadır.

Sikloid eğrisi sadece dünyamıza ait bir şekil değildir. Sikloid şekli, Jüpiter’in uydusu Europa’nın çatlayan buz yüzeylerinde uydu görüntülerinden görülebiliyor. Çatlama, ayın Jüpiter etrafındaki yörünge yoluna ve bunun sonucunda ortaya çıkan yerçekimi basıncına karşılık gelir.

Kaynaklar ve ileri okumalar
- The curved history of cycloids, from Galileo to cycle gears. Bağlantı: https://www.irishtimes.com/
- Shirali, Shailesh. (2013). Marin Mersenne, 1588–1648. Resonance. 18. 10.1007/s12045-013-0034-2.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel