Matematikte en ilgi çeken sayılardan biri pi sayısıdır fakat en az onun kadar önemli bir sabit daha vardır. Bu sabit ise adını fazla kimsenin duymadığı e sayısıdır. Bazı matematikçilerin Euler sayısı olarak da adlandırdığı Euler sabiti 2,718281… olarak başlar ve diğer aşkın sayılar gibi sonsuza kadar devam eder.
Nüfus artışını belirlemede, finansal matematikle uğraştığımız zamanlarda, olasılık ve istatistik hesaplamalarında e sayısı sıkça karşımıza çıkar. Aslında yaşamda değişim ya da büyümeyi içeren bir şey yapmak istediğimizde muhtemelen arka planda bir yerlerde bu sayı gizlidir.
e Sayısı Nedir?

Bu sorunun cevabını vermeden önce böyle bir sabite neden ihtiyaç duyduğumuza anlayarak işe başlamalıyız. 16. ve 17. yüzyılların bilimsel devriminde, güvenilir bir hesaplama aracının olmaması ilerlemenin önüne bir engeldi.
Sayıları çarpıp bölme işlemini toplama çıkarma işlemine dönüştüren ve dolayısıyla işlemlerin çok daha hızlı yapılmasını sağlayan yöntemleri geliştiren ilk kişinin İskoçyalı Baron John Napier (1550-1617) olduğu kabul edilmektedir. Bu işleme logaritma adını takan da Napier’dir.

Napier logaritmasını temelinde üçgen çözümlemelerinde kullanılan denklemlerin çözümünü kolaylaştırmak için hazırlanmıştı. Tabloları bu tip sorularda işe yarıyordu. Devamında matematikçiler bu tabloları daha işlevsel hale getirme yarışına başlayacaklardı.
Yine de onun adıyla anıyor olmamız gereken logaritmaya doğal logaritma ya da Napier logaritması dendi. Bugün lnx biçiminde gösterdiğimiz bu logaritma aslında hiç de doğal olmayan bir biçimde Euler’in e sayısı kullanılır. Onun kaldığı yerden 1600’lerin sonlarında, İsviçreli matematikçi Jacob Bernoulli devam etti. Bileşik faizi hesaplamak için 2.718… kullandı.
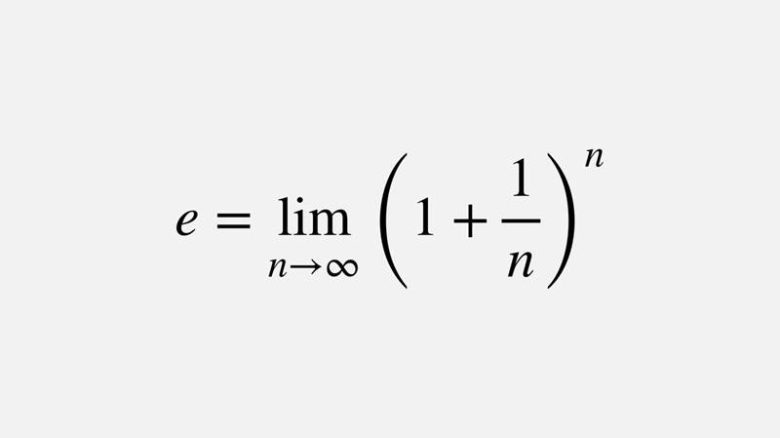
Ancak e sayısının ne olduğunu ilk kez düşünen kişi Leonhard Euler oldu. Sayının Euler sabiti olarak anılmasının da nedeni de budur. Euler bu sayıyı 18 ondalık basamağa kadar hesapladı ve konu üzerine ilk çalışmasını 1727 yılında yazdı. Bu hesaplamayı da aşağıda gördüğünüz formül ile gerçekleştirdi.
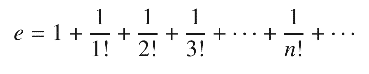
Euler, e’yi 18 ondalık basamağa kadar hesapladıktan sonra sayının irrasyonel bir sayı olduğunu anladı. 1873’te Fransız matematikçi Charles Hermite, e’nin cebirsel olmadığını yani aşkın bir sayı olduğunu kanıtladı. Bunun anlamı şuydu. Bir denklemi çözerek bu sayının hesaplanması imkansızdı.
Aşkın sayıları keyfi bir biçimde karıştırmaya başlarsak zorluklarla karşılaşırız. Örneğin e + π sayısının aşkın olup olmadığı bile bilinmemektedir. πe aşkın bir sayıdır, fakat aynı şeyin eπ için söylenip söylenemeyeceği bilinmemektedir.
e Sayısı ile Bileşik Faiz Nasıl İlişki İçindedir?
İki tür faiz vardır, basit faiz ve bileşik faiz. Basit faiz yönteminde anapara sabit kalmakta böylece her dönem elde edilen faiz geliri de aynı olmaktadır. Bileşik faiz yönteminde ise her dönem elde edilen faiz anaparaya eklenir. Sonraki dönemler için faiz artan anapara üzerinden hesaplanır.
Öncelikle 100 liramız olduğunu düşünelim ve %100 faiz oranına sahip bir bankaya 1 yıllığına yatıralım. Yatırdığımız 100 liramız bize 1 yıl sonunda 200 lira olarak geri dönecektir. Şimdi parayı 6 aylığına %50’den faize yatıralım ve 6 ay sonunda elimize geçen paranın tamamını tekrar 6 aylığına %50’den faize yatıralım. Bu durumda 150+75 = 225 liramız olacaktır.
Şimdi paramızı 3’er aylık dönemlerde %25 faizle bankaya yatıralım. Benzer hesaplamaları yapacak olursak 100 liramızın 244,141 lira olduğunu görürüz. Eğer bu işi her ay tekrarlarsak 100 liramız 261,304 lira olur. Paramız gittikçe artıyor diye düşünebilirsiniz ama bununda bir sınırı vardır o sınır da e sayısıdır.
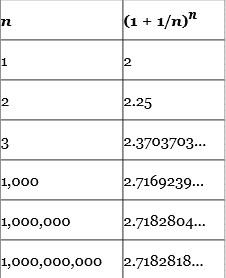
İmkansız elbette ama paranızı saniyeler içinde yatırıp çekip tekrar yatırabilseydiniz yıl sonunda elinize geçen para 271,828 lira olacaktır. Bunu genellemek için oluşturulan bir de formül vardır. Bu formül bize e sayısının değerini yaklaşık olarak değerini verecektir. Detaylar burada: Bileşik Faiz İle Euler Sayısının İlişkisi Nedir?
Toplam Para: Yatırılan Para.( 1+1/n)n
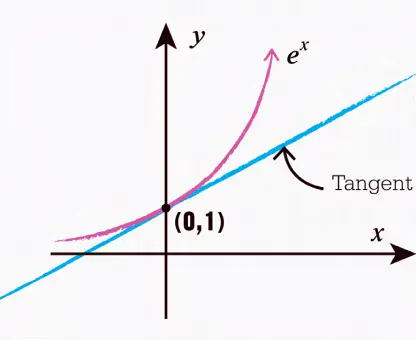
Büyüme Eğrisi
Yukarıda örneğini verdiğimiz bileşik faiz hesaplaması üstel büyümeye bir örnektir. Bu tür bir büyüme bir grafik üzerinde çizilir ise bize bir eğri olarak görünecektir. Üstel fonksiyon, y eksenini (0,1)’de kesen ve giderek daha dik hale gelen y = ex eğrisini üretir. Aşağıda görmüş olduğunuz bu eğri bazı özelliklere sahiptir. Örneğin, y = ex grafiği, (0,1) noktasında, eğimi 1 olan doğruya teğettir. Bunun nedeni, ex‘in türevinin (değişim oranı) aslında ex olmasıdır.
Euler Sabiti Beklemediğimiz Yerlerde Karşımıza Çıkabilir
Bir dizi öğenin sıralanabileceği çeşitli yollara permütasyon denir. Örneğin 1, 2, 3 kümesi 1, 3, 2 veya 2, 1, 3 veya 2, 3, 1 veya 3, 1, 2 veya 3, 2, 1 olarak sıralayabiliriz. Bunu kısaca 3! (3 × 2 × 1) biçiminde gösteririz. Euler sayısı, düzensizlik adı verilen bir permütasyon türünde de önemlidir. Bir düzensizlikte, öğelerin hiçbiri orijinal konumlarında kalamaz.
Bu düzensizliklerin hesaplanması az elemanlı kümelerde deneme yoluyla hesaplansa da eleman sayısı arttıkça işler zorlaşır. İşte burada işin içine yine e sayısı girer. Bu sayı, herhangi bir kümedeki düzensizliklerin sayısını hesaplamayı mümkün kılar. Sonuç, e’ye bölünen ve en yakın tam sayıya yuvarlanan permütasyon sayısına eşittir. Örneğin 1, 2, 3 kümesi için, en 6 ÷ e = 2.207 yani yaklaşık 2’dir.
Euler, borçlarını ödemek için bir piyango yaratmayı planlayan Prusya Kralı Büyük Frederick için 10 sayının düzensizliğini analiz etmişti 10 sayı için Euler, bunun sonucunun 1⁄e olduğunu bulmuştu.
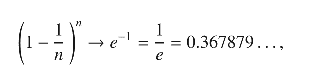
İlginç bir şekilde, bu 1 / e değeri, genellikle “sekreter sorunu” olarak bilinen başka bir alışılmadık durumda ortaya çıkar. Belirli bir iş için çok sayıda aday arasından bir sekreter seçmek istediğinizi ve bunun için mülakat yaptığınızı varsayalım. Doğru karar verebilmek için kaç aday ile mülakat yapmamız gerekir?
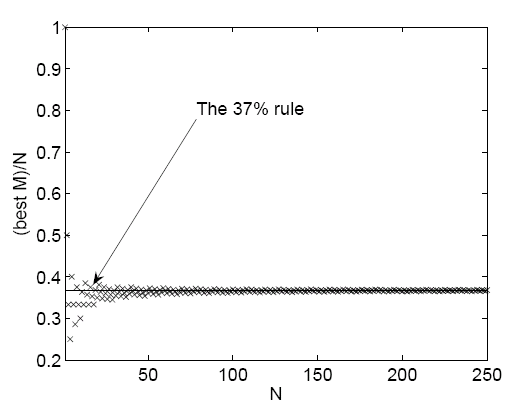
Görünüşe göre en iyi strateji ilk 1/e başvuranlarla (toplam başvuru sayısının yaklaşık % 37’si) kadar mülakat yapmaktır. Göz atabilirsiniz: Matematikçiler, Hayatınızın En Önemli Kararları İçin % 37 Kuralını Öneriyorlar
Kaynaklar ve ileri okumalar:
- Joel L. Schiff, The Mathematical Universe: From Pythagoras to Planck; Springer Praxis Books
- Reichert, S. e is everywhere. Nat. Phys. 15, 982 (2019). https://doi.org/10.1038/s41567-019-0655-9
- What’s the Big Deal With Euler’s Number?;Yayınlanma tarihi: 2 mart 2021; Bağlantı: https://www.popularmechanics.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel