Hepimiz düz bir çizginin iki nokta arasındaki en kısa yol olduğunu kabul ederiz. Ancak en kısa yol her zaman en hızlı olan mıdır? Soruya ve konuya yabancı olanları için Brakistokron (Brachistochrone) problemi ve eğrisi ile tanıştıralım.

Konunun detaylarına geçmeden önce aşağıdaki görselde gördüğünüz A ve B noktalarının arasında bir eğik düzlem olduğunu ve bir topu sadece yerçekimi etkisi (sürtünme veya hava direncinin olmadığı varsayılarak) ile A noktasından B noktasına en hızlı biçimde göndermek istediğinizi düşünelim.
Bu iniş süresini en aza indirecek eğrinin şekli nedir? Bu soru Brakistokron ( Brachistochrone) problemi olarak bilinir. Sorunun cevabı da elbette Brakistokron eğrisi olacaktır. ( Yunanca asıllı bir kelime olan Brachistochrone, “en kısa zaman” anlamına geliyor.)

Meşhur Bernoulli kardeşlerden Johann Bernoulli’nin 1696’da ortaya attığı bu problem, dönemin matematikçilerine için açık bir meydan okumaydı. Daha da önemlisi, Johann Bernoulli’nin dünyaya ne kadar büyük bir matematikçi olduğunu göstermesi için bir şanstı. İddiasına göre Bernoulli bu problemi iki haftalık bir çalışma sonunda çözmüştü. Şimdi de diğer matematikçileri çözüme dahil etmek, biraz da ne kadar iyi bir matematikçi olduğunu göstermek istiyordu.
Probleme gönderilen çözümlerden biri ağabeyi Jacob Bernoulli’ye aitti. Matematikçi Gottfried Leibniz de bir çözüm gönderdi. Bir başka çözüm de Fransız matematikçi Guillaume de l’Hôpital’den geldi. Newton da, kısa sürede oyuna dahil oldu. Soruyu bir gecede çözdü ve isimsiz olarak gönderdi. Bernoulli daha sonra çözümün Newton’dan geldiğini bildiğini tahmin edecekti. Bir çok matematikçi soruyu çözmüş olsa da, Bernoulli’nin çözümü şaşırtıcı derecede basitti.
Brakistokron Problemi İçin Johann Bernoulli’nin Bulduğu Çözüm
Aslında Johann Bernoulli, brakhistokron problemini ilk düşünen kişi değildi. 1638 yılında Galileo Discourse on two new sciences adlı kitabında aynı problemi sormuştu. Ancak çözümünde hata yapmıştı. Ona göre cevap bir çember yayı olmalıydı. Çözümün detaylarına geçmeden önce bir kere daha şekle dikkat edelim.
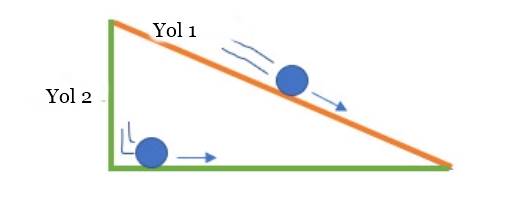
Görselde topu yuvarlamanın iki farklı seçeneğini görüyorsunuz. Aklımıza ilk gelen 1. yoldaki topa yerçekimi bir miktar etki etse de, 2. yoldaki top başlangıçta direk yerçekimi etkisi ile serbest düşüş yapacağı için 1. yoldakinden daha yüksek bir hıza ulaşır, devamında yolculuğuna devam eder. Yani aslında eğik düzlem üzerindeki toptan daha hızlı biçimde hedefine ulaşır. Ancak bir yol olarak düşündüğümüzde bunun uygulaması olası değildir. Ya iki ile birleştirirsek ne olur? Aslında bu sorunun cevabını aşağıda görebilirsiniz.
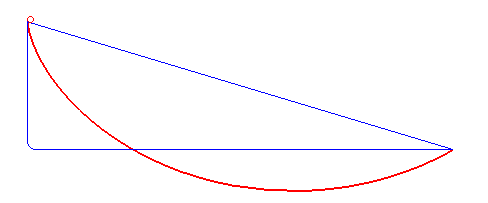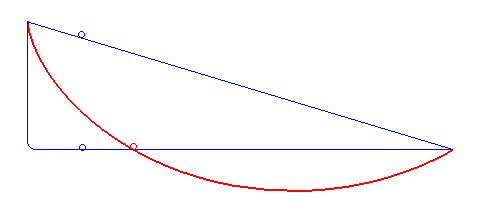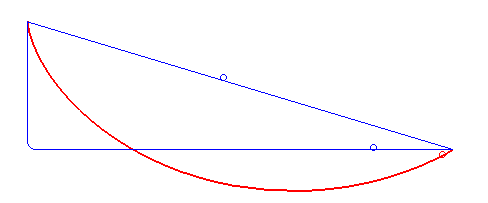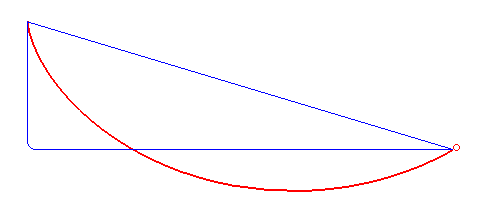
Bernoulli, bu sorunu çözmenin harika bir yolunu düşündü. Sorunun cevabı aslında ışığın doğasında saklıydı. Hepimizin lise fizik dersinde öğrendiği kırılmalar ile ilgili bir doğa gerçeği Bernoulli’yi zamanının en iddialı matematikçilerinden biri olduğunu doğruluyordu.
Snell yasası, ışığın farklı yoğunluklara sahip iki ortam arasında geçerken kırılma açısının nasıl değiştiğini tanımlayan bir optik yasadır. Bu yasa, Hollandalı bilim insanı Willebrord Snellius (veya Snell) tarafından 1621 yılında geliştirilmiştir.
Brakistokron Problemi İle Snell Yasası Neden İlişkilidir?
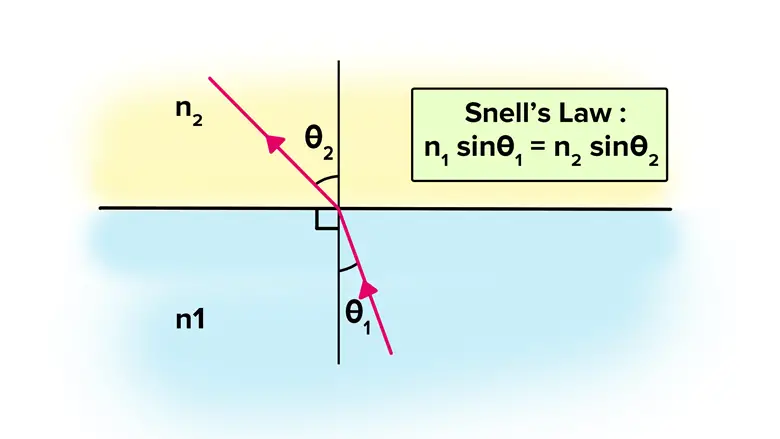
Yukarıdaki yasa neticesinde de gördüğümüz gibi ışık belirli bir yol boyunca ilerlerken farklı hızlarda hareket eder. Işık her zaman Snell yasasına uyar ve kırılır çünkü hedefine en kısa yoldan ulaşmak ister. Brakistokron problemini çözmek için Bernoulli bu gerçeği fark edecekti. Işığı bir değil birden çok ortamdan arka arkaya geçirirsek yani peş peşe kırılmasına izin verirsek ortaya çıkan eğrinin şekli neye benzer sorusunun cevabını bulmak istedi. Aşağıdaki görselde de gördüğünüz gibi bu eğri Brakistokron eğrisi idi.
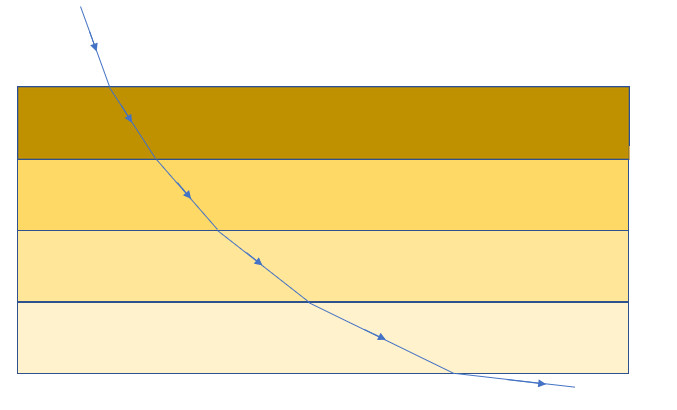
Bernoulli bu eğrinin başka biçimde tanımlanabileceğini de fark edecekti. Aslında bu eğri sikloid eğrisi ile de ilişkiliydi. Bir bisiklet tekerleğinin kenarına küçük bir ışık taktığınızı hayal edin. Şimdi uzaktan bir yerden, bisikletin hareketi esnasında nasıl bir şekil ortaya çıktığına bakın. Göreceğiniz şey aşağıdaki görseldekine benzeyecektir. Bir doğru boyunca dönerek ilerleyen bir çemberin üzerindeki sabit bir noktanın takip ettiği yola sikloid eğrisi denir. Bu nedenle, sikloid mümkün olan en hızlı yoldur ve Brakistokron sorununun çözümüdür.

Sikloidler, son 500 yılda birçok önde gelen bir çok matematikçi tarafından incelenmiştir. ancak bugünkü ismini veren de Galileo’dur. Düşen bir nesneyi ışık ile birleştirerek elde ettiği çözüm de Bernoulli’nin gerçekten 17. yüzyıl matematikçileri arasında bir efsane olduğunun bir kanıtı gibidir. Yazının devamı için buraya göz atabilirsiniz. Galileo’dan Bisiklet Dişlilerine Sikloid Eğrisi
Kaynaklar ve ileri okumalar:
- Is The Shortest Path Always The Fastest?; https://www.scienceabc.com/
- The brachistochrone problem; Bağlantı: https://mathshistory.st-andrews.ac.uk/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









