Doğal sayılar, tam sayılar. Hepimiz bir çok sayı kümesini tanıyoruz. Ancak aşkın sayılar diğer adı ile transendental sayılar kulağa oldukça yabancı geliyor. Aslında hepimizin bildiği e sayısı ve π sayısı aşkın sayıdır. Ancak bizler gibi matematikçilerin de bu sayıları anlaması yüzyıllar alacaktı.
Matematikçi Leopold Kronecker, “Sayıları Tanrı yarattı, ötekilerin tümü insanların işidir” sözü ile anımsanmaktadır. Bu durum gerçekten de doğrudur. Her sayı kümesinin, kendi içinde büyüleyici ve karmaşık bir geçmişi vardır. Bugün okullarımızda doğal sayılardan başlayarak, tamsayılar, rasyonel sayılar biçiminde birbirini kapsayan sayı ailelerini öğretiyoruz. Bunu da belli bir mantıkla yapıyoruz.
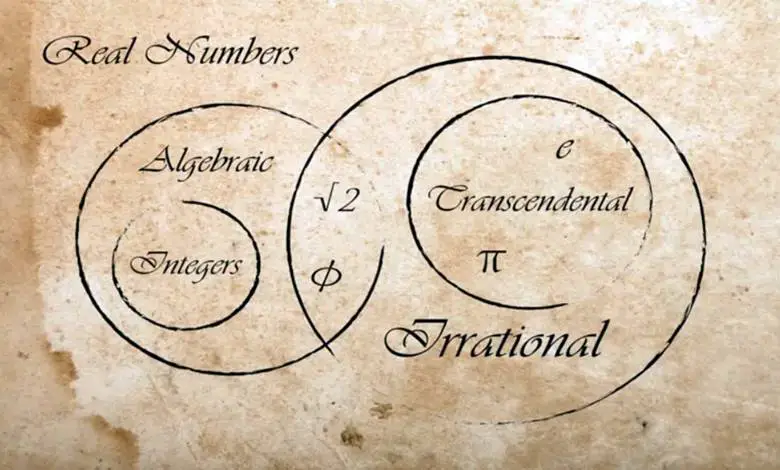
Bildiğiniz gibi rasyonel sayılar, 3, −1/2 ve 57/22 gibi tam sayıların birbirine bölümü olarak ifade edilebilen sayılardır. Ondalık açılımları ya sona erer (−1/2 = −0.5) ya da sonsuza kadar devam eder (57/22 = 2.509090909…). Bu sonsuza kadar devam eden sayıları da irrasyonel sayılar olarak isimlendiririz. Rasyonel ve irrasyonel sayılar birlikte reel sayıları oluşturur. Lise yıllarına geldiği zaman da öğrenciler, reel sayılar ve hayali sayıların birleştirilmesiyle oluşan karmaşık sayıları öğrenirler;
Bunların hepsini zaten biliyorduk demeniz olasıdır. Peki ama yazımızda ele alacağımızdan bahsettiğimiz aşkın sayılar nerede? Aslında bu sorunun cevabını anlamak için kısa bir süre geçmişe, bu sayıların çıkış noktasına bakmamız gerekecek.
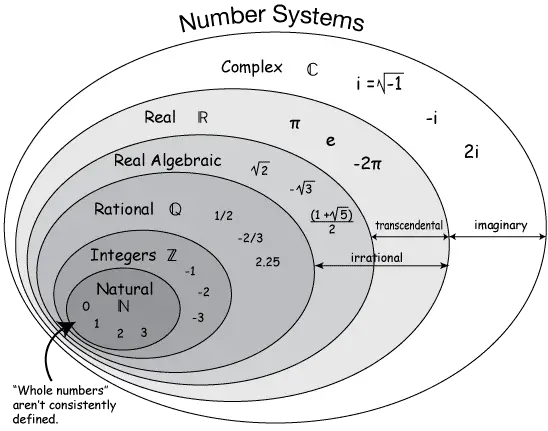
Cebirsel ve Aşkın sayılar Nedir?
Günlük dilde “aşkın” kelimesi, sıradanlığın ötesinde, gizemli bir şeyi ifade eder. Öte yandan matematikte “aşkın” teriminin anlamı daha dünyevidir. Basitçe ax 3 + bx 2 + cx + d = 0 gibi polinom denklemlerinin çözümleri olamayacak sonsuz sayıdaki sayıların sınıfını tanımlar.
Katsayısı rasyonel sayı olan bir polinomun kökü (çözümü) olan sayılara bir cebirsel sayı adı verildi. Örneğin x-3=0 denkleminin kökü olan 3 bir cebirsel sayıdır. (Tüm tam sayılar ve doğal sayılar birer cebirsel sayıdır.) Ayrıca 2x=1 ifadesinin çözümü olan 1/2 bir cebirsel sayıdır. (Tüm rasyonel sayılar da cebirsel sayılardır.)
Cebirsel sayı olan irrasyonel ifadeler de vardır zira √2 sayısı x2-2=0 polinomunun köküdür. Tüm rasyonel sayıların ve bir takım irrasyonel sayıların cebirsel sayılar olduğunu gördükten sonra akla bir soru geliyor. Cebirsel olmayan sayılar var mı? Sorunun yanıtı cebirsel olmayan sayılar yani aşkın sayılardı. Yani aslında reel sayılar kümesi cebirsel sayılar ve aşkın sayılar biçiminde de ikiye ayrılmaktadır.
Aşkın Sayıların Varlığının Anlaşılması Antik Çağ Problemlerinden Birinin Çözümü İle Mümkün Olacaktı
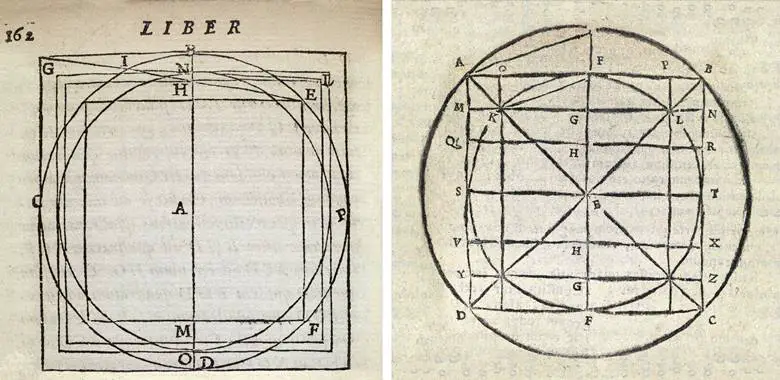
Yalnızca bir pergel ve bir cetvel kullanarak, belirli bir çemberle aynı alana sahip bir kare çizebilir misiniz? Çemberi karelemek olarak bilinen bu soru, ancak cebirin icadından ve herhangi bir çemberin çevresinin çapına oranı olan π sayısının daha iyi anlaşılmasından sonra yanıtlandı.
Muhtemelen en ünlü aşkın sayı pi sayısıdır, sonrasında da e sayısı gelecektir. Matematikçiler en başından beri pi sayısının diğer irrasyonel sayılardan farklı olduğunun farkındaydı. Ancak cebirsel ve aşkın sayılar kavramlarını ilk kez 18. yüzyılda Leonhard Euler tanımlanana kadar konu ile ilgili bir gelişme yaşanmayacaktı.
Ancak 1882 yılında Alman matematikçi Ferdinand von Lindemann pi sayısının aşkın bir sayı olduğunu kanıtladı. Bu önemli bir gelişmeydi. Lindeman bunu yaptığında tarihin bilinen en eski matematik problemini de çözmüş oluyordu. Pi sayısının bir aşkın sayı olduğu gerçeği, antik çağın en ünlü sorunlarından birinin yani çemberi karelemek sorunsalının asla çözülemeyeceği anlamına da geliyordu.
Belirli bir sayının cebirsel mi yoksa aşkın mı olduğunu söylemek ise kolay bir iş değildir. En ünlü iki irrasyonel sayı hepimizin bildiği pi sayısı ve e sayısıdır. Her ikisinin de aşkın olduğu bilinmektedir. Buna rağmen π + e ile π x e sayılarının aşkın olup olmadığını bilmiyoruz. Ancak ilginç bir biçimde eπ sayısının aşkın olduğunu biliyoruz.

Aşkın Sayılar İçin Genel Bir Çözüm Bulma Uğraşı
Zaman içinde matematikçiler daha çok aşkın sayı arayışı içine girdiler. Bunun için yeni bir yaklaşım biçimine ihtiyaç vardı. Alman matematikçi David Hilbert, 1900’deki Uluslararası Matematikçiler Kongresi’nde önümüzdeki yıllarda matematikçiler tarafından ele alınması gerektiğini düşündüğü problemler listesini sunduğunda bu ihtiyacı dikkate aldı.
Aşkın sayıları oluşturmak için bir yöntem bulmak bu listedeki yedinci problemdi. Hilbert’in bu yedinci sorunun nasıl çözülebileceğine dair bir varsayımı vardı. Buna göre a’nın bir cebirsel sayı olduğunu (0 ve 1 hariç) ve b’nin irrasyonel bir cebirsel sayı olduğunu varsayalım. Euler tarafından yapılan benzer bir varsayımdan yola çıkarak Hilbert bu durumda ab‘nin zorunlu olarak aşkın bir sayı olduğu varsayımında bulundu.

Yedinci soru, bunun kesin bir kanıtını bulmaktı. Doğru olduğu kanıtlanabilseydi, örneğin 2 √2 sayısı 2 ya da ‘nin ne de √2 aşkın olmadığı halde aşkın olurdu. Böylece matematikçiler, daha fazla aşkın sayılar elde edebilirdi. Sonunda yedinci problemin kesin bir kanıtını sunan kişi Rus matematikçi Aleksandr Osipovich Gelʹfond oldu. Kendisi 2 √2 sayısının aşkın bir sayı olduğunu kanıtladı. 1934’te tam bir çözüm yayınladı.
Böylesine önemli bir varsayımın ispatı, normalde yazarının uluslararası matematikte merkezi bir aşamaya gelmesini sağlamalıydı ama olmadı. Savaş zamanlarıydı ve Gel’fond da dahil olmak üzere SSCB’den matematikçilerin seyahat izinleri yoktu.
Matematikçiler, çözümün yazar tarafından bir karatahtada sunulduğunu görmek yerine okumakla yetinmek zorunda kalacaklardı. Bazen Gel’fond varsayımı olarak adlandırılan, Hilbert’in yedinci probleminin çözümünün, 1970 yılında İngiliz matematikçi Alan Baker için matematikteki en prestijli ödüllerden biri olan Fields Madalyası kazandırdığını belirtmek düşündürücüdür.
Kaynaklar ve ileri okumalar:
- Transcendental Numbers; Bağlantı: https://brilliant.org/
- Maths in a minute: Transcendental numbers (and politics); Yayınlanma tarihi: 31 Ağustos 2018; Bağlantı: https://plus.maths.org/
- How Math Achieved Transcendence. Yayınlanma tarihi: 28 Haziran 2023; Bağlantı: https://www.quantamagazine.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









