
Asal sayılar eskilerden beri sadece matematikçilerin değil, bilim ile yolu kesişen tüm insanların ilgisini çekmiştir. Bunun temel nedeni tüm pozitif tamsayıların, asal sayılardan oluşturulabilmesidir. Bu nedenle de asal sayılar bir yerde tamsayıların temel yapı taşları gibidir.
2000 yıldan daha uzun bir süre önce, Öklid sonsuz sayıda asal sayı olduğunu kanıtlamıştı, (İspatı için buraya bakın). Ancak bir sayının asal sayı olup olmadığını bize söyleyen basit bir formül hala elimizde yok. Günümüzde bilgisayar algoritmaları, giderek daha büyük asal sayıları bulmamızı sağlasa da elimizde bir formül olmadığı için hiçbir zaman hepsini yazamayacağız. Neyse ki asal sayı teoremi bize asal sayıların diğer tam sayılar arasında nasıl dağıldığı hakkında bir şeyler söyler.
Asal Sayı Teoremi Nedir?

Asal sayı teoremi bize verilen herhangi bir pozitif reel sayıya eşit veya ondan küçük olan asal sayıların sayısını verir. Başka bir deyişle bir pozitif n tamsayısı verildiğinde, n’ye kadar ve n dahil kaç tam sayı asal sayı olduğunu söyler.
Ancak asal sayı teoremi bunu tam olarak yanıtlamaz. Bunun yerine yaklaşık bir değer verebilir. Basitçe söylemek gerekirse, n tamsayısı için n/ ln(n) n dahil ve n’ye kadar olan asal sayıların sayısı için iyi bir tahmindir ve n büyüdükçe tahmin daha doğru olur.
Örnek olarak, n=1.000 alalım. 1.000’e kadar (bu listeden bakabilirsiniz) asal sayıların gerçek sayısı 168’dir. Tahminimiz ise 1000/ln(1000) hesaplaması sonucunda yaklaşık olarak 145 yapar. Gerçek değer 168 ve bizim bulduğumuz yaklaşık değer ise 145 idi. Bu ikisini birbirine oranlarsak 145/168 sonucu 0,86 yapacaktır. Diğer bir deyişle tahminimizin gerçek sonucun %86 kadarını bilebildiğini anlarız. Bu çok da fena sayılmaz.
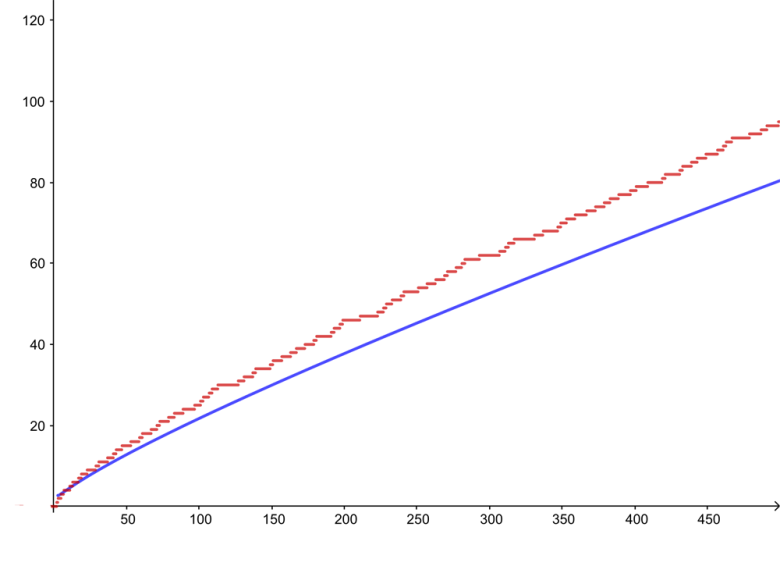
Bir başka örnek verelim. Bu sefer n=100.000 alalım. Bu sayıya kadar normalde 9.592 tane asal sayı vardır. n= 100.000 değerini formülümüzde yerine yazarsak da yaklaşık 8686 elde ederiz. Bu iki değeri birbirine oranlarsak da 8686/ 9592 sonucu bize yaklaşık 0,9 verecektir. Bu mevcut asal sayıların %90’ını bulabildiğimiz anlamına gelir. Kesinlikle biraz önceki tahminden daha iyidir.
Bu nedenle asal sayı teoremi bize büyük n değerleri için n/log (n) hesaplamasının gerçek değerin %100’üne yakın olduğunu söyler. Yeterince büyük n değerleri seçerseniz sonucun neredeyse %100 olmasını sağlayabilirsiniz.
Asal Sayı Teoreminin Genellenmesi
Daha genel bir biçimde ifade etmek gerekirse asal sayı teoremi aşağıdaki formüldeki gibi ifade edilir. π (n) n’den küçük veya ona eşit olan asal sayıların sayısı anlamına gelmektedir. Buradaki π ifadesinin bizim bildiğimiz π sayısı ile bir ilgisi yoktur.
π (n) asal sayı sayma fonksiyonu gibi düşünülmelidir. Örneğin, π(10) = 4 olur. Çünkü 10’a eşit veya daha küçük dört asal sayı vardır (2, 3, 5 ve 7). Benzer şekilde, π(100) = 25 tir. Çünkü ilk 100 tam sayının 25’i asaldır.
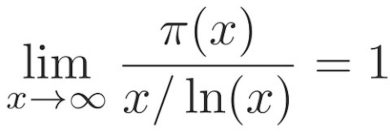
1 trilyona kadar sıralı bir pozitif tamsayı listeniz olsa bile, kimse manuel olarak kaçının asal sayı olduğunu belirlemek istemez. π(1,000,000,000,000) burada devreye girer. Teorem bize π(n)’nin n/ ln(n)’ye “asimptotik olarak eşit” olduğunu söyler. (Asimptotik bir eşitliği yaklaşık bir eşitlik olarak düşünebilirsiniz, ancak teknik olarak bundan daha fazlasıdır.) 1 triyonu teoremde yerine yazarsak gerçek yanıttan yalnızca yaklaşık %4 oranında hata payı oluşur. Bu da oldukça iyi bir tahmindir.
Asal sayı teoreminin kesin formülasyonu, hatta ispatının ayrıntıları, burada tartışamayacağımız kadar ileri düzeyde matematik gerektirir. Ancak bilmeniz gereken fikir asal sayı teoreminin, asal sayıların pozitif tam sayılar arasında asimptotik dağılımını tanımlamaya yaradığı biçiminde olacaktır.
Asal sayıların büyüdükçe daha az yaygın hale geldiğini biliyoruz. Peki, 1.000.000 ile 1.001.000 arasında kaç tane asal sayı vardır. İşte bunu asal sayı teoremi ile tahmin edebiliriz.
Asal Sayı Teoremi İle Nasıl Tanıştık?
Hesaplamalar, sayılar büyüdükçe asal sayıların giderek daha nadir hale geldiğini ortaya koyuyordu. Ancak tam olarak ne kadar nadir olduklarını ifade edecek doğru bir teorem ifade etmek mümkün müdür? Bu sorunun cevabı Carl Friedrich Gauss tarafından 1793’te verildi. Ancak teoremin resmi bir kanıtı ancak yaklaşık 100 yıl sonra, hem de birbirinden habersiz iki matematikçi Fransız Jacques Hadamard ve Belçikalı de la Vallée-Poussin tarafından yapılacaktı.

Devamında bir çok matematikçi asal sayıların dağılımı ile ilgili çalışmalar yaptı. Bunlardan birisi de Bernhard Riemann idi. Aslına bakarsanız asal sayıların incelenmesini içeren sayı teorisi, yüzlerce yıldır en büyük beyinler tarafından başarısız bir şekilde ele alınan çözülmemiş problemlerle doludur. Muhtemelen matematikteki en ünlü çözülmemiş problem olan Riemann’ın hipotezi Bernhard Riemann tarafından 1859’da önerildi.
Riemann hipotezi de özünde asal sayılar daha ziyade asal sayıların sayı doğrusu üzerine dağılımı ile ilgilidir. Bu neden önemli? Kimi ilgilendirir?
Matematikçiler problemlerini her şeyden önce zorluklarına ve içsel güzelliklerine göre yargılarlar. Asal sayılar bu kriterlerin her ikisinde de yüksek puan alır. Bununla birlikte, asal sayılar pratik bir şekilde de faydalıdır. Asal sayılar üzerine yapılan araştırmalar, son birkaç on yılda şifrelemede önemli bir kullanım bulmuştur. Yazının devamında göz atmak isterseniz: Riemann Hipotezi: Dünyanın En Zor ve Ünlü Problemi
Kaynaklar ve ileri okumalar:
- Marianne on August; Maths in a minute: The prime number theorem. Yayınlanma tarihi: 25Ağustos 2021; Yayınlandığı Yer: plus.maths; Bağlantı: https://plus.maths.org
- Mathematicians Will Never Stop Proving the Prime Number Theorem. Yayınlanma tarihi: 22 Temmuz 2020. Yayınlandığı Yer: Quantamagazine.; Bağlantı: https://www.quantamagazine.org/
- de Shalit E (2018) Prime Numbers–Why are They So Exciting?. Front. Young Minds. 6:40. doi: 10.3389/frym.2018.00040
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









