Regiomontanus Problemi Nedir? En İyi Görüntüleme Açısı Nasıl Bulunur?

Regiomontanus adını bugüne kadar duymamış olmanız normaldir. Ancak adını duymasanız bile muhtemelen ortaya attığı problemi deneyimlemiş olmalısınız. Sinemada film izlerken hangi koltuğu seçmeniz ya da fotoğraf çekerken hangi noktadan çekmeniz gerektiği gibi durumları düşünürken aklınıza Regiomontanus problemi gelmelidir.

Duvara bir resim asmak istediğiniz de ya da satın aldığınız yarım boy aynadan tüm vücudunuzu görmek için tam olarak nereye asmanız gerektiği konusunda karar vermeniz gerektiği zamanlarda da bu problem işinize yarayabilir. Yeterince ilgi çekebildiysek anlatmaya başlayalım.

Yüzyıllar boyunca bir çok matematikçi Euclid’in elemanlar eserini okuyarak geometri ve matematik öğrendiler. Birçok fizikçi ve astronom ise bu kitabın metodolojisini örnek alarak alanlarıyla ilgili kitaplar yazdılar.

Bu eseri okuyanlar ise hem eserin muhteşem oluşundan etkilendiler hem de bir süre sonra yeni sorular sorma ihtiyacı hissettiler. Bu şekilde de yeni keşiflerde bulundular. Örneğin 1471’de Alman matematikçi Johann Müller (Regiomontanus) bir arkadaşına aşağıdaki soruyu yönelttiği bir mektup yazdı: “Yer üzerindeki hangi noktadan yere dikili bir çubuk en büyük görünür?”.

Bu problem elbette cebirsel olarak çözülebilir, ancak bu Regiomontanus için bu seçenek mevcut değildi! Çünkü daha cebirin ortaya çıkması için 200 sene vardı. Dahası, tamamen geometrik bir çözüm daha basit ve daha zarifti. Temelde hepsinin ana düşüncesi aynı olmakla beraber zamanla bu sorunun farklı versiyonları ortaya çıktı. Heykel problemi, Ragbi problemi bunlardan bir kaçı. Şimdi bu iki problem üzerinde Regiomontanus’un ortaya attığı problemini anlamaya çalışalım.

Bir heykel hangi mesafeden (noktadan) en net görünür?

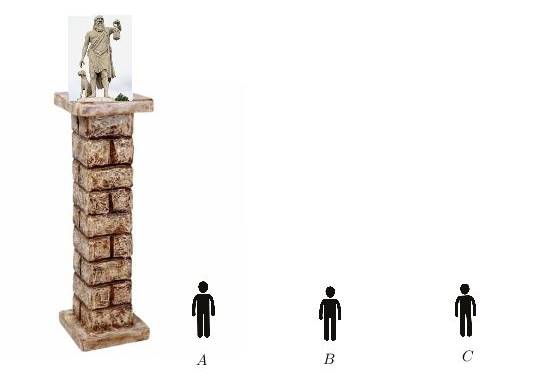
A noktasında bulunan seyircinin yerine kendimizi koyalım ve düşünelim. İlk olarak heykele çok yakınız ve boynumuzu kaldırmamız gerekir. Bu da bize konforsuz bir bakış açısı sunar. Bundan çok daha önemlisi ise heykeli görmek için çok dar bir açıya sahip oluruz. C noktasında bulunan seyirci açısından olaya bakarsak bu seferde gözlerimizi heykeli görmek için çok zorlarız. Bu da görüntü netliği açısından bazı dezavantajlar sunar. A noktasındaki seyircinin düşmüş olduğu durum ise en kötüsüdür.

Sonuçta heykeli görmek için çok dar bir açıya sahip oluruz. Sizin de tahmin etmiş olacağınız gibi en ideal nokta B noktasıdır. Bu noktadan heykeli tam bir biçimde görme seçeneğimiz olur. Ancak işin önemli kısmı şudur. Bu noktayı geometri yardımı ile bulabilir miyiz?

Cevap elbette evet olacaktır. Bu nokta, heykelin tepe ve taban noktaları ile bu heykelin izlenileceği noktanın tam olarak bir çemberin üzerine denk düştüğü yerdir. Aşağıdaki resim bize bu durumu daha net gösterecektir. Bu cevap, Elemanlar’ın üçüncü kitabı olan Çemberler’de bulunmaktadır. 

Bu problem, antik çağlardan beri matematik tarihinde ortaya çıkan ilk optimizasyon problemiydi. Muhtemelen o dönemin Rönesans sanatçılarının uğraştığı perspektif sorularından ilham almıştı. Modern matematik ders kitaplarında genellikle şu şekilde karşımıza çıkar. Bir tablo duvarda düz biçimde asılıdır. Görüş açısını en üst düzeye çıkarmak için duvardan ne kadar uzakta durmak gerekir? Problemin başka bir türevi de aşağıdaki gibidir.

Ragbi oyuncusunun sayı yapmak için kaleye en iyi mesafesi neresidir?

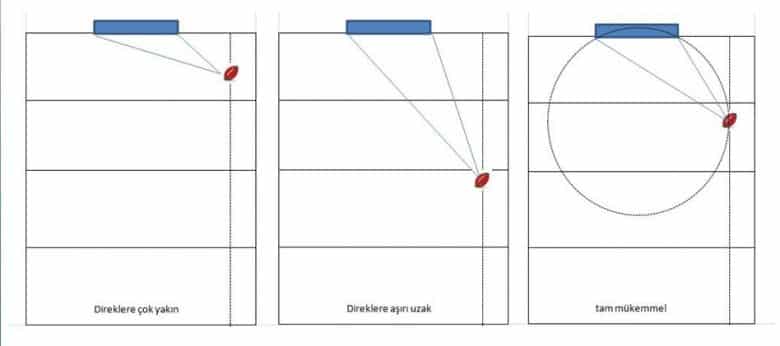
Eğer karşı kaleye çok yakınsanız açı çok dardır, fakat çok uzaksanız açı yine azalacaktır. En iyi pozisyon neresidir o halde? Burada sahaya havadan bakmamız ve diğerine benzer bir diyagram çizmemiz gerekir. Mümkün olan en net atış noktalarını gösteren noktalı çizgilerin en açık olduğu yer çemberin kalenin iki ucundan ve doğrunun geri kalan kısmından geçtiği yerdir.

Yukarıda aktardığımız problemlerin hepsinin cebirsel çözümü elbette mümkündür. Ancak Regiomontanus tarafından ortaya atılan çözüm kesinlikle daha yaratıcıdır. Bundan sonra siz siz olun sinemada film izlerken hangi koltuğu seçmeniz gerektiğinde ya da seyahat esnasında fotoğraf çekerken hangi noktadan çekmeniz gerektiği durumda bu problemin çözümünde kullanılan yönteme başvurun. Zararlı çıkmazsınız. Ayrıca merak ederseniz: Standart En Boy Oranı Neden 16:9 Biçimindedir?

Kaynaklar ve ileri okumalar

1. Bellos, Alex (2012). Alex Sayılar Diyarında. (İstanbul: Pegasus Yayınları)
2. Wells, David (1998). Geometrinin Gizli Dünyası. (çev. Selçuk Alsan), (İstanbul: Sarmal Yayınevi)
3.  Historical Activities for Calculus – Module 3: Optimization – Regiomontanus’ Hanging Picture Problem; https://www.maa.org/

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel