
Bazen doğru olduğundan şüphelendiğimiz (ama henüz kanıtlayamadığımız) bir şey aslında yanlış olsaydı ne olurdu diye kendi kendimize sorarız. Bu sorumuzun klasik mantıktaki karşılığı olarak düşünebileceğimiz reductio ad absurdum diğer bir deyişle olmayana ergi, çok eskiden beri bilinen bir ispat yöntemidir. Bu yöntem gündelik yaşantıda da sıklıkla kullanılmaktadır.
Bu yöntemin son derece kullanışlı bir ispat biçimi olmasının bir nedeni, doğrudan ispatlanamayan bir yargının doğruluğu konusunda bu yöntemle karar verilebilmesidir. Reductio Ad Absurdum, mantıklı bir sonuca varmanın saçmalığını göstererek bir argümanı çürütür. Ancak bu, yalnızca başlangıçtaki argümanda hatalı mantık varsa işe yarar.
Matematikte ispatlar temelde ikiye ayrılır. Doğrudan ve dolaylı olmak üzere. Olmayana ergi, dolaylı ispatlar kategorisinde kendine yer bulur. Matematiksel ispatlarda çok sık kullanılan bu yol şu anlama gelir: Bir p önermesini ispatlamak için, p’nin tersini varsaymak ve ondan bir çelişki çıkarsamak yeterlidir.

Tarihsel sürecin matematikteki ispatlara da yön verdiğini düşünmekteyim. Daha doğrusu bir ispat 2000 yıldır tazeliğini koruyorsa bunun hikayesinin, ispat şeklinin önemi yadsınamaz bir gerçektir. Örneğin kök2 nin rasyonel bir sayı olmadığının ispatı ya da asal sayıların sonsuzluğunun ispatı bu yöntem sayesinde yapılabilmiştir.

Olmayana Ergi Yöntemi İçin Bir Örnek
Asal sayıların sonsuzluğunu Olmayana ergi yöntemi ile gösterelim. Bu durumda doğru kabul edeceğimiz önerme : ‘Sonlu sayıda asal sayı vardır.’ olacaktır. Bu önermeyi doğru kabul ettiğimize göre en büyük asal sayı olmak zorunda. Bu asal sayıya pn diyelim. Şimdi şöyle bir x sayısı tanımlayalım, x sayısı bütün asalların çarpımından bir fazla olsun.
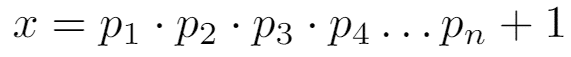
Görünen o ki, x sayısı hiçbir asal sayıya tam bölünemiyor, hep 1 kalan veriyor. Buradan şu sonuç çıkar: x de bir asal sayıdır. Fakat x bariz bir şekilde pn asalından (en büyük asaldan) büyük. Bu bir çelişkidir. Demek ki sonsuz sayıda asal vardır. Gördüğünüz gibi, bir ifadenin “yanlış” olduğunu varsaymak suretiyle yapılacak bir denetleme onun tüm mümkün doğruluk durumlarının “doğru” olup olmadığını tek tek denetleme uğraşından çok daha pratik görünmektedir.
Matematikteki kalıpları farkında olarak veya olmayarak günlük yaşantımızda kullanırız. Reductio ad absurdum tekniği de bir yönüyle mizah alanında kendini bizlere gösterir: Acayip bir önerme ele alınır. Şaka ya da fıkra bu öncülü saçma bir noktaya kadar geliştirir. Ya da akla uygun ama mecazi anlamda söylenen bir önerme asıl anlamında yorumlanır ve fıkra buna uygun olarak geliştirilir.
Örneğin, bir çok mizah öyküsü “şöyle şöyle olsaydı ne olurdu?” anlamına gelen paragraflarla başlar. Burada “şöyle şöyle olsaydı” tümcesi saçma sonuçları öykünün devamında geliştiren öncüldür. Mizahta vurgulanan şey doğal olarak matematiktekinden farklıdır. Mizahta, öncülüğü saçmalığa indirgemek, öncülü reddetmek amacından çok, saçmalığın kendisi için yapılır. Yine de hicivde olduğu gibi, iki amaç bir arada bulunabilir. Hocanın fıkralarından birine veya birkaçına bu bakış açısıyla bakmak size kalsın….
Kaynakça:
- Bir matematikçinin savunması, G. H. Hardy; 2008; Tübitak yayınları
- Matematik ve Mizah, J. A. Paulos; 2003; Doruk Yayınevi
Dip Not:
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım
Matematiksel





