Okul yıllarından geriye aklınızda bir parça matematik kaldı ise bu muhtemel Pisagor teoremidir. Pisagor teoremi devamında öğretmenler öğrencilere, bazı sıralı üçlüleri ezberlemelerini öğütlerler. Bu sıralı üçlüler Pisagor Üçlüsü olarak bilinirler.
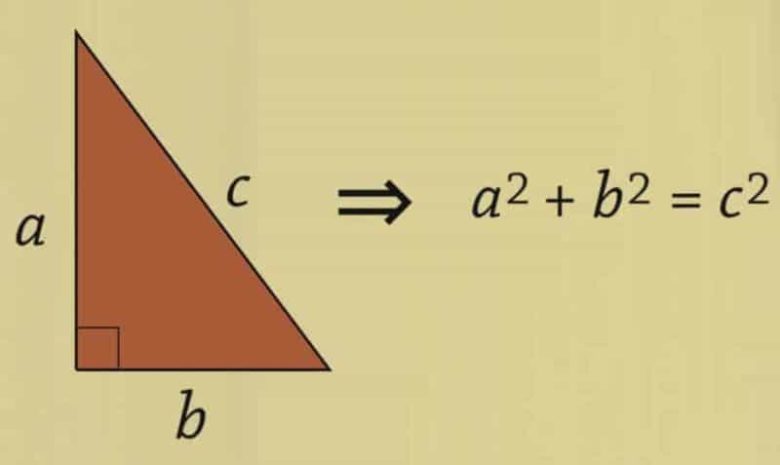
Bir Pisagor üçlüsünde en büyük sayı hipotenüstür. Hipotenüsü 100’den küçük olan bazı Pisagor üçlüleri aşağıdaki gibidir.

Yukarıdaki listeye dikkatle bakarsanız kırmızı ve mavi ile yazılmış olan bazı üçlülerin birbirinin katı olduğunu fark edersiniz. Geometrik olarak, eğer bir Pisagor üçlüsü diğerinin katıysa, karşılık gelen üçgenler benzerdir. Bir Pisagor üçlüsü başka bir Pisagor üçlüsünün katı değilse, o zaman bunun temel üçlü olduğunu söyleriz. Örneğimizde (3, 4, 5) temel bir Pisagor üçlüsü iken (6, 8, 10), (9, 12, 15) ve (12, 16, 20) değildir.
Diğer antik Yunan matematikçilerinin yanı sıra Pisagor’un kendisinin de ilgisini çeken bir soru, Pisagor üçlülerinin nasıl oluşturulacağıdır. Diğer bir deyişle, size pozitif bir a sayısı verirsek, bir Pisagor üçlüsü oluşturacak şekilde iki b ve c sayısını bulabilir misiniz? İşte bu okul matematiğinde nadiren bahsedilen bir başlıktır. Aslında bunun için kullanabileceğimiz bir kaç metot vardır.
Pisagor Üçlülerini Nasıl Oluşturabiliriz?

Pisagor teoremini sağlayan (a, b, c) ve ( A, B, C) tamsayılarımız olsun. Bu ikisini aşağıda gördüğünüz biçimde bir araya getirerek yeni bir Pisagor üçlüsü elde edebilirsiniz.
(a.A-b.B)^{2}+(a.B+b.A)^{^{2}}=(c.C)^{2}Hemen (3, 4, 5) ve (5, 12, 13) üçlülerini deneyelim. Bu durumda aşağıdaki sonucu elde ederiz.
(3.5-4.12)^{2}+(3.22+4.5)^{^{2}}=(5.13)^{2}\Rightarrow (15-48)^{2}+(36+20)^{^{2}}=(65)^{2}Gördüğünüz gibi (33, 56, 65) Pisagor üçlüsünü yarattık. Ancak bu teknik modern zamana ait sanıyorsanız yanılıyorsunuz. Aslında konu ile ilgili ilk açıklamalar bizzat Pisagor’un kendisi tarafından yapılmıştır. Sonrasında da Öklid kendisi açıklamasını getirmiştir. Şimdi bunun nasıl olduğunu anlatmaya çalışalım. Öncelikle Pisagor teoremini yazalım ve aşağıdaki biçimde düzenleyelim.
a^{2}+b^{2}=c^{2} ; c^{2}-b^{2}=a^{2}Şimdi aşağıda gördüğünüz iki özdeşliği düşünelim. Sizin de fark ettiğiniz gibi bu özdeşlikler sadece tek bir işaret ile birbirinden farklıdır.
(a^{2}+1)^{2}=a^{4}+2a^{2}+1 \:ve\: (a^{2}-1)^{2}=a^{4}-2a^{2}+1
Yukarıdaki özdeşlikleri birbirinden çıkarırsak 4a^2 elde ederiz. Bu durumda aşağıdaki aşağıdaki eşitliği de yazabiliriz. Aşağıdaki ikilinin arasındaki fark da a^2 kadar olacaktır.
\frac{(a^{2}+1)^{2}}{4} \: ve \: \frac{(a^{2}-1)^{2}}{4}Şimdi kendimize b ve c değerleri seçmemiz gerekiyor. Yukarıdaki ikiliden bir tanesinin b^2 diğerinin de c^2 olduğunu kabul edelim. Bu durumda b ve c değerlerini aşağıdaki gibi düşünebiliriz. Üstelik a, b ve c’nin Pisagor üçlüsünü sağlaması için tamsayılar olması gerektiğini biliyoruz. Bu durumda b ve c nin çift sayı olması gerektiğini de anlarız. Bu durumda da a’nın tek sayı olması gerekecektir.
b=\frac{(a^{2}-1)}{2} \: ve\: c=\frac{(a^{2}+1)}{2}Tek sayılar için Pisagor üçlülerini nasıl yazacağımızı artık biliyoruz. Sonuçta aşağıdaki biçimde düşünürsek bir üçlü elde edebiliriz.
a=a \:;\: b=\frac{(a^{2}-1)}{2} \: ve\: c=\frac{(a^{2}+1)}{2}Aslına bakarsanız a’nın çift olduğu durumlarda, Pisagor üçlülerini bulmak için de, basit bir yöntem vardır. Bu sefer elde etmek istediğimi Pisagor üçlüsünün (2a ,2b, 2c) biçiminde olduğunu kabul edelim. Yukarıda elde ettiğimiz sonuçtan devam edeceğiz. Bu sefer seçeceğimiz a, b ve c ise aşağıdaki gibi olacak.
a_{1}=2a\: ; \: b_{1}=2b=a^{2}-1=\left ( \frac{a_{1}}{2} \right )^{2}-1\: ve\: c_{1}=2c=a^{2}+1=\left ( \frac{a_{1}}{2} \right )^{2}+1Yani a çift ise, Pisagor üçlülerini bulmak için, ilk verilen sayının yarısının karesinden bir çıkartmak sayılarımızdan birini, bir toplamak ise diğer sayımızı verecektir. Aşağıdaki tabloda çift ve tek Pisagor üçlülerini görüyorsunuz. İsterseniz yukardaki formüller yardımı ile deneyebilirsiniz. Bu arada çift Pisagor üçlülerini bulma yönteminin de Platon tarafından ilk olarak ortaya konduğunu da anımsatalım.
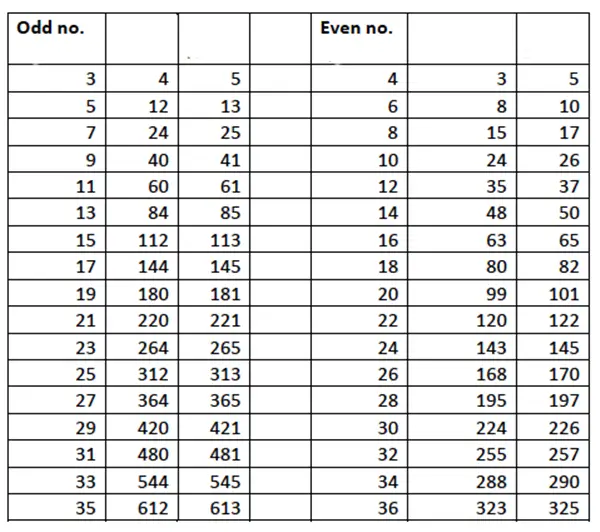
Tüm Pisagor Üçlülerini Bu Biçimde Hesaplayabilir miyiz?
Yukarıdaki yöntemler yardımı ile gördüğünüz gibi bir çok Pisagor üçlüsü elde ettik. Peki hepsini bulabilirdik mi? Ne yazık ki hayır. Dikkatli bir okur listede (20, 21,29)’un eksik olduğunu fark edecektir. Aslına bakarsanız Öklid de bu eksiği fark etmişti ve bize genel bir formül vermişti. Bunun için m>n biçiminde iki pozitif m ve n tamsayısı düşünelim. Aslında bundan sonraki süreç biraz da yukarda açıkladığımız gibi ilerleyecek. Öncelikle aşağıdaki iki açılımı yazacağız.
\left ( m^{2}+n^{2} \right )^{2}=m^{4}+2m^{2}n^{2}+n^{4}\: ve\: \left ( m^{2}-n^{2} \right )^{2}=m^{4}-2m^{2}n^{2}+n^{4}Sonrasında da yine uygun a, b ve c üçlüsünü seçmemiz gerekiyor. Sonuçta aşağıdaki genel formülü kullanarak tüm Pisagor üçlülerini bulabilirsiniz.
a=m^{2}-n^{2}\: ;\: b=2mn \: ve\: c=m^{2}+n^{2}\:Bonus: Pisagor Dörtlüleri
Gördüğünüz gibi Öklid’in öngörüsü bize tüm Pisagor üçlülerini verecektir. Şimdi üç yerine dört pozitif tam sayıdan oluşan Pisagor dörtlülerine bakalım. Bir Pisagor dörtlüsünde ilk üç sayının karelerinin toplamı bize dördüncünün karesini verir. Bir Pisagor dörtlüsü nedir ve ne işime yara derseniz aşağıdaki şekle bakmanızı öneririz. Gördüğünüz gibi bir dikdörtgenler prizmasının cisim köşegeni aslında Pisagor dörtlüleri tarafından hesaplanır. ( Ancak bu bilgi okullarda pek anlatılmaz)
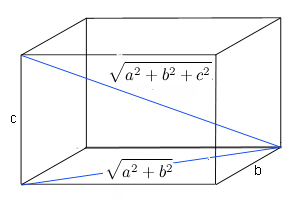
Daha önce olduğu gibi, eğer (a, b, c, d) bir Pisagor dörtlüsü ise, herhangi bir pozitif k tam sayısı için (ka, kb ,kc, kd) de öyledir. Diğer bir deyişle a, b ve c’nin en büyük ortak böleni 1 ise dörtlümüz temeldir. Aşağıda bazı örnekler görebilirsiniz. Aynı renkte olanlar birbirinin katı olan dörtlüleri göstermektedir.

Az önce aktardığımıza benzer bir süreç aracılığı ile Pisagor dörtlülerinin diğerlerini de keşfetmemiz mümkündür. Peki işi biraz daha ileri taşırsak ne olur? Ya küpleri alsaydık?
Kübik Dörtlüler
Elbette bu noktadan sonrasına okullarda ihtiyaç duymazsınız. Ancak arka planda neler olup bittiğini görmek güzel bir öngörü kazandırır. Aşağıda gördüğünüz sayılara kübik dörtlüler denir. (1,6,8,9), (3,18,24,27), (3,4,5,6) kübik dörtlülere vereceğimiz bir kaç örnektir.
a^{3}+b^{3}+c^{3}=d^{3}Onları burada nasıl oluşturacağımızı keşfetmeyeceğiz. Bunun yerine daha ilginç olduğu ortaya çıkan bir soru soracağız: Kübik üçlüler de var mı? Bu soru, matematiğin en ünlü sorularından birisidir. Bu da bizi Fermat’ın son teoremine bağlar. Bu da galiba Pisagor üçlülerini daha da özel yapıyor.
Kaynaklar ve ileri okumalar:
- Triples and quadruples: from Pythagoras to Fermat.; Yayınlanma tarihi: 14 Kasım 2012; Bağlantı: https://plus.maths.org/
- Mathematicians Shed Light on Minimalist Conjecture. yayınlanma tarihi: 9 Temmuz 2013. Kaynak site: Quanta magazine. Bağlantı: Mathematicians Shed Light on Minimalist Conjecture
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel