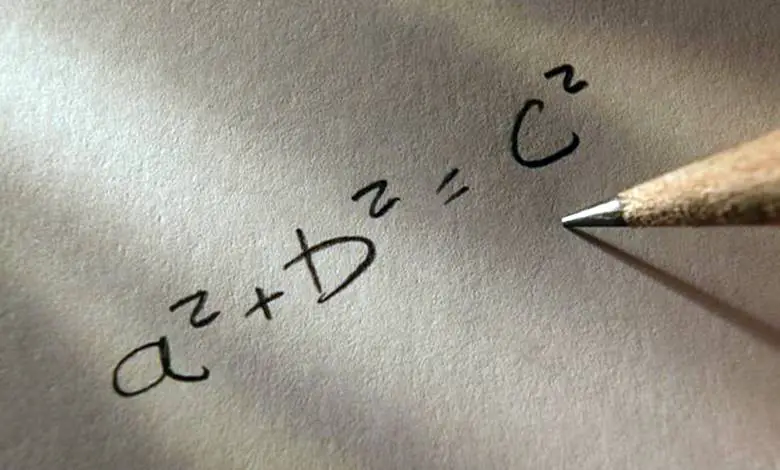
Bugün ulaştığımız uygarlık seviyesinde Pisagor’un rolünü inkar edemeyiz. Ancak elbette onun en önemli mirası, adıyla anılan o meşhur Pisagor Teoremidir. Bu teorem bir dik üçgende kenarların karelerinin toplamının hipotenüsün karesine eşit olduğunu söyler ve cebirsel olarak a ve b kenarlar olmak üzere, a2 + b2 = c2 biçiminde gösterilir. Teorem Pisagor’un adını taşısa da aslında bu teoremi kendisi bulmamıştır. MÖ 1900-1600 yıllarından kalma dört Babil tabletinde de bu teoreme rastlanmaktadır.

Pisagor‘un hayatının belli bir döneminde düşüncelerini geliştirmek için yolculuklar yaptığını biliyoruz. Kendisinin bu teorem ile bu esnada tanışmış olması muhtemeldir.
Öyle görülüyor ki sadece bir içgüdü ile doğruluğu önceden kabul edilen bu kural, yüzyıllar boyunca uygarlıktan uygarlığa dolaşmış ve sonunda Pisagor’un karşısına çıkmıştır. Pisagor teoremi bir çok antik uygarlık tarafından Pisagor’dan önce bilinir olsa da bunun ilk pratik uygulaması Mısır’da karşımıza çıkar.
Mısır Üçgeni

MÖ 2000’li yıllarda geometrinin doğduğu topraklarda yaşayan Mısırlılar üçgenler ve piramitler hakkında bazı geometrik fikirlere sahiptiler. Ancak bunları yazılı olmaktan ziyade pratik biçimde uygulamaya koydular. Örneğin İp germe, piramitler gibi yapıların inşasında dik üçgen elde etmek için kullanılan bir yöntemdi. Zaten Hipotenüs kelimesi de Yunanca ‘karşılıklı gerilen’ kelimesinden gelmektedir.
Mısırlılar bunun için uzunluğu 12 birim olan düğümlü bir ip kullanırlardı. Bu tür iplerle kenarları 3:4:5 birim olan dik üçgenler yaptılar. Sonra da bu ipler yardımıyla arazileri ölçtüler. İp germe mirasından dolayı, 3:4:5 oranındaki dik üçgen Mısır üçgeni olarak da bilinir.
Pisagor Teoremi İspatları
Pisagor teoremine evrensel çekiciliğini veren şey kuşkusuz ki yüzyıllar boyunca önerilen çok sayıda ispatıdır. Bu teoremini ispat etmek için trigonometri veya analitik geometri kullanılamaz. Zira, onların da oluşumları zaten Pisagor eşitliğine bağlıdır.
Amerikalı matematikçi Elisha Scott Loomis, bir çok matematik kitabı yazmıştır. Ancak bunlar içinde en dikkat çekeni iki bölüm halinde yayınlanan The Pythagorean Proposition ( Pisagorcu Önermeler) isimli kitabı olmuştur.
Kitapta 109 cebirsel ispat ve 255 geometrik ispat olmak üzere toplam 370 ispat bulunmaktadır. (Ayrıca 4 kuaterniyonik ve 2 dinamik ispat vardır, toplamda 370 yapar). İspatların bazıları üçgenlerin benzerliği, bazıları parçalara ayrılıp incelenmesi, bazıları cebirsel formülleri çok azı da vektörlerin kullanımına dayanır. Bu ispatlardan üçünü aşağıda görebilirsiniz.
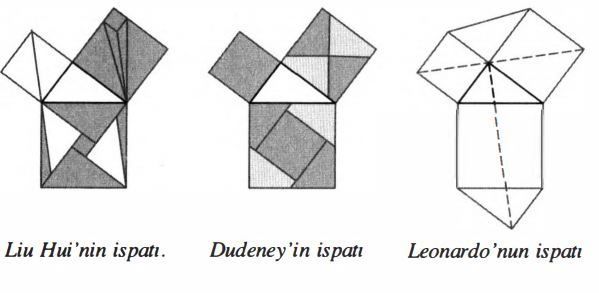
Dokümanlara dayanılarak bilinen ilk tam geometrik çözümün, Euclid tarafından verildiğini kabul etmek durumundayız. Bütün klâsik geometri kitaplarında bugün, tarihi değeri bakımından, sadece Euclid’in verdiği çözüm öğretilmektedir. Pisagor’un bu teorem için yaptığı bir ispat olup olmadığı bilinmemekte ancak olmadığı düşünülmektedir.
Öklid’in Kitabında Yer Alan Pisagor Teoreminin İspatı
ABC, BAC açısı dik açı olan bir dik açılı üçgen olsun. BC kenarı üzerine BDEC karesini, BA ve AC kenarları üzerine de GB ve HC karelerini çiz. AL doğru parçasını BD veya CE ye paralel olacak şekilde çiz. AD ile FC yi çiz.
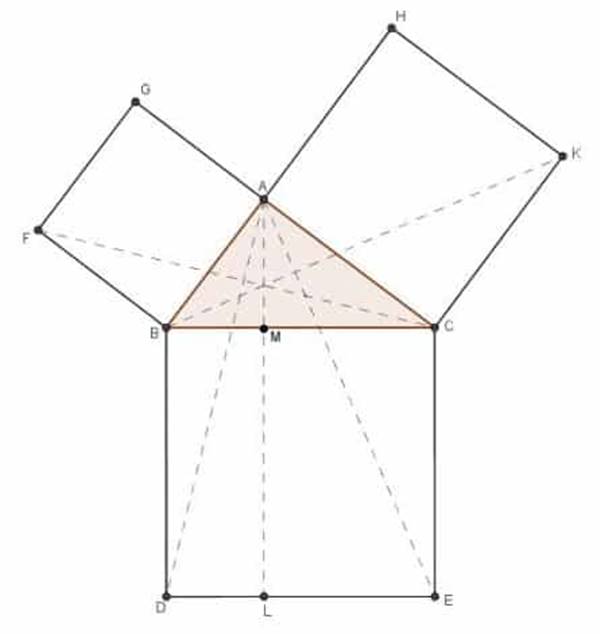
BAC ve BAG dik açılardır. BA doğru parçası A noktasında AC ve AG kenarları ile yapmış oldukları komşu açıların toplamları iki dik açıya eşit olduğundan CA ve AG doğru parçaları aynı doğrultudadır. Aynı sebepten BA ile AH da aynı doğrultudadır. DBC ve FBA açıları birbirine eşit olan dik açılardır. Her birine ABC açısını ekleyelim. Bu durumda DBA açısı da FBC açısına eşit olur.
DB kenarı BC kenarına, FB kenarı BA kenarına eşittir. AB ve BD kenarları, sırasıyla FB ve BC kenarlarına eşit ve ABD açısı FBC açısına eşit olduğundan AD kenarı da FC kenarına eşittir ve ABD ile FBC üçgenleri ile eştir.
Aynı BD ve AL paralel kenarlar altında aynı BD tabanına sahip olduklarından dolayı BL paralelkenarının alanı ABD üçgeninin alanının iki katıdır, Yine aynı FB ve GC paralel kenarlar altında aynı FB tabanına sahip olduklarından dolayı GB karesinin alanı FBC üçgeninin alanının iki katıdır.
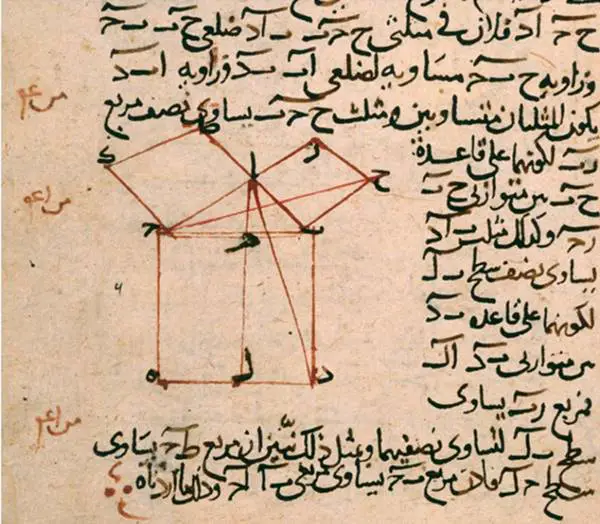
Bu durumda BL paralelkenarının alanı GB karesinin alanına eşittir. Benzer olarak AE ve BK kenarları çizilirse, CL paralelkenarının alanı HC karesinin alanına eşittir. BDEC karesinin alanı GB ve HC karelerinin alanları toplamına eşittir.
BDEC karesi BC kenarı üzerine, GB ve HC kareleri BA ve AC üzerlerine kuruludur. Buradan BC kenarının karesi BA ve AC kenarlarının kareleri toplamına eşittir. Bu yüzden bir dik üçgende dik açının karşısındaki kenarın karesi dik açıya komşu olan kenarların karelerinin toplamına eşittir. Q.E.D
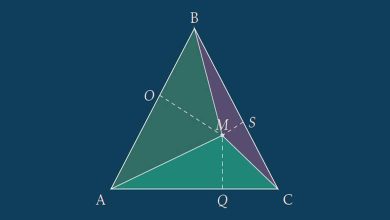
James Garfield’in İspatı En Kolay İspattır
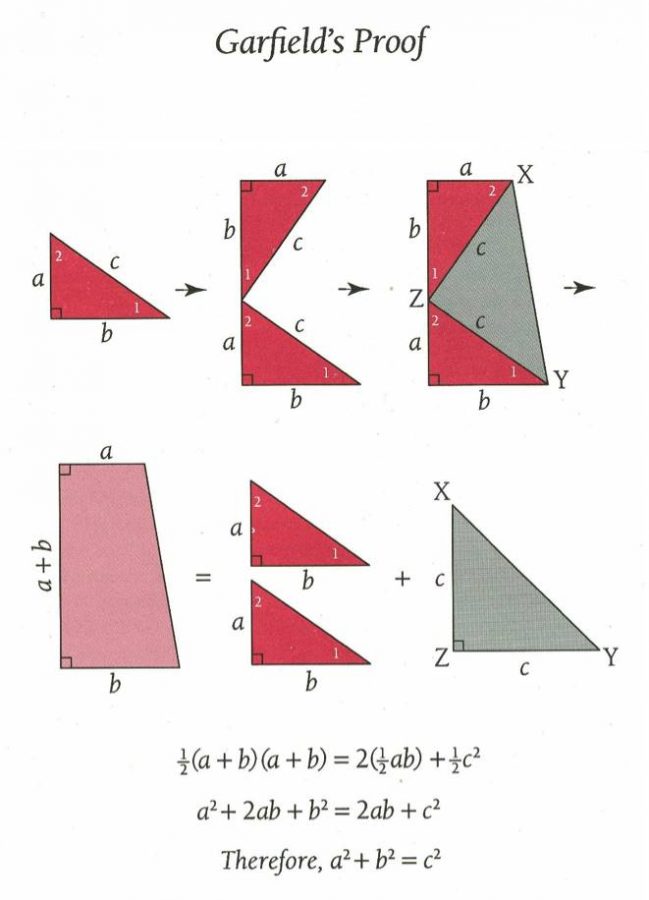
Bir başka ilginç ispat ise Ann Condit adlı Amerikalı bir genç kızın yaptığıdır. Henüz 16 yaşında bir lise öğrencisi iken 1938 yılında yaptığı ispatta kullandığı geometrik çizimi, hiçbir ünlü matematikçi tarafından daha önce düşünülmemiştir.
Amerika Birleşik Devletleri’nin 20. Başkanı James Garfield bile Pisagor teoreminin ispatlarından birini gerçekleştirmiştir. Tüm ispatlar arasında Garfield’in yaklaşımı en basit ve anlaşılması en kolay olanlardan biridir.
Pisagor Teoremi Günümüzde Ne İşe Yarar?
Pisagor teoremi sadece ilgi çekici bir matematiksel alıştırma değildir. İnşaat ve imalattan navigasyona kadar çok çeşitli alanlarda kullanılmaktadır. Ayrıca dağlar gibi standart yollardan ölçülmesi mümkün olmayan yükseklikleri ölçmek için de haritacılar Pisagor teoreminden yararlanır.
Tek tek listelemeye gerek yok. Açılarınız olduğunda ve ölçümlere ihtiyacınız duyduğunuzda hangi konu ile ilgilenirseniz ilgilenin bu teoreme ihtiyacınız vardır. Bir daha ki sefere karşınıza bir Pisagor teoremi çıktığında uğruna verilen bunca çabayı hatırlamanız dileğimizle. Ayrıca göz atmak isterseniz: Ezber Yapmadan Pisagor Üçlüleri Nasıl Bulunur?
Kaynaklar ve ileri okumalar için:
- Pythagorean theorem; https://www.britannica.com/
- Pythagorean Theorem; https://www.cut-the-knot.org
- Elisha Scott Loomis; https://en.wikipedia.org/
- How many ways are there to prove the Pythagorean theorem? ; https://www.youtube.com/watch?v=YompsDlEdtc
- The Pythagorean Theorem Makes Construction and GPS Possible; https://science.howstuffworks.com/
Matematiksel