Muhtemelen lise yıllarında hepimiz logaritma ile tanıştık ve gerekli işlemleri yapmak için bazı kurallarını ezberledik. Ancak sonrasında bir daha da düşünmek zorunda kalmadık. Sonuçta günlük hayatımızı sürdürmek için logaritmaya pek de ihtiyaç duyulmuyor gibi gözüküyor. Peki durum gerçekten bu mu? Gelin logaritma nedir, ne değildir bir kere daha anımsayalım.
Binlerce yıl boyunca matematikçiler çoğu hesaplamayı sadece sayma tahtaları veya abaküs gibi aletler kullanılarak elle yaptılar. Bu işlemler esnasında özellikle çarpma ve bölme işlemi daha uzun zaman alıyordu.
Günümüzde bize sadece derslerde ezberlenmesi gereken bir dizi sıkıcı kurallar gibi gelse de logaritma insanlığın teknoloji ile tanışmadığı dönemlerde hesaplama yapabilmenin tek yoluydu. Logaritma temelinde çarpmayı toplamaya çevirir, çok büyük ve çok küçük sayıları karşılaştırmamıza yardımcı olur.
Logaritmayı Kim Buldu?
16. ve 17. yüzyılların bilimsel devriminde, güvenilir bir hesaplama aracının olmaması ilerlemenin önüne bir engeldi. Sayıları çarpıp bölme işlemini toplama çıkarma işlemine dönüştüren ve dolayısıyla işlemlerin çok daha hızlı yapılmasını sağlayan yöntemleri geliştiren ilk kişinin İskoçyalı Baron John Napier (1550-1617) olduğu kabul edilmektedir.
Bu işleme logaritma adını takan da Napier’dir. “Oran” anlamına gelen Yunanca logos kelimesi ile “sayı” anlamına gelen arithmos kelimelerini birleştirip logarithmus kelimesini türetmiştir. (Harizmi’nin adından türetilen algoritma kelimesinin logaritmayla bir ilgisi yoktur.)
Napier çalışmalarının sonuçlarını 1614 yılında Mirifici Logarithmorum Canonis Descripto adı altında yayımladığında büyük sansasyon yaratmıştı.

Napier’in bu çalışmasını gören Pierre-Simon Laplace’ın Napier için “birkaç ayda bitecek hesapların süresini birkaç güne indirerek astronomların hayatını ikiye katladı ve onları bu çeşit hesaplarda hata yapıp mahcup olmaktan kurtardı” demesi çalışmasının dönemin koşullarında ne denli önemli olduğunu bizlere göstermektedir.
1960’lardan itibaren hesap makinesi ve bilgisayarın hayatımıza girmesiyle logaritmayı elle hesaplamaya ihtiyaç azalsa da birçok fiziksel ve biyolojik sürecin davranışı logaritmik olduğu için logaritma halen matematiğin içinde önemini korumaktadır. ( Göz atmak isterseniz: Çarpma İşlemi Yapmak İçin En Hızlı Yöntem Nedir?)
Logaritma Nedir?
Bunu bir matematiksel bir formül ile ifade etmemiz gerekirse: log (x.y)= log x + log y kullanırız. Peki bunu nasıl yapar derseniz öncelikle Napier’in logaritmayı düşünce biçimini anlamanız gerekir. Bunun günümüzde yaptığımız tanımdan oldukça farklı olduğunu fark edeceksiniz.
Napier, logaritmalarını oluşturmak için iki paralel çizgi boyunca hareket eden iki parçacığı hayal etti. İlk satır sonsuz uzunluktayken ikincisi ise on milyon birim uzunluktaydı. Her parçacık aynı başlangıç pozisyonunu aynı anda ve aynı hızda yola çıktı.

Sonsuz uzunluktaki çizgi üzerindeki parçacık ( A) tekdüze bir hareket yapmak zorundaydı. Yani eşit zamanlarda eşit mesafeler kat etti. İkinci parçacığın (B) hızı, çizginin sonuna kadar kalan mesafe ile orantılıydı.
A ve B noktalarının geçtikleri mesafeleri eşit zaman aralıklarında ölçersek, A noktası aynı zaman aralıklarında hep aynı mesafeyi geçerken, B noktasının bir zaman aralığında gittiği mesafe bir önceki zaman aralığında gittiği mesafenin sabit bir oranı kadardır.
Yani A noktasının başlangıçtan itibaren gittiği mesafe aritmetik bir dizi halinde artarken B noktasının gittiği mesafe geometrik bir dizi olarak artmaktadır. B noktasının hızı her an önünde kalan mesafeyle orantılı olarak azalacak şekilde tanımlanır.
Napier herhangi bir zamanda B noktasının önünde kalan mesafenin logaritmasını, A noktasının o ana kadar geçtiği mesafe olarak tanımlar. Böylece on milyona kadar olan tüm pozitif sayıların logaritması tanımlanmış olur.
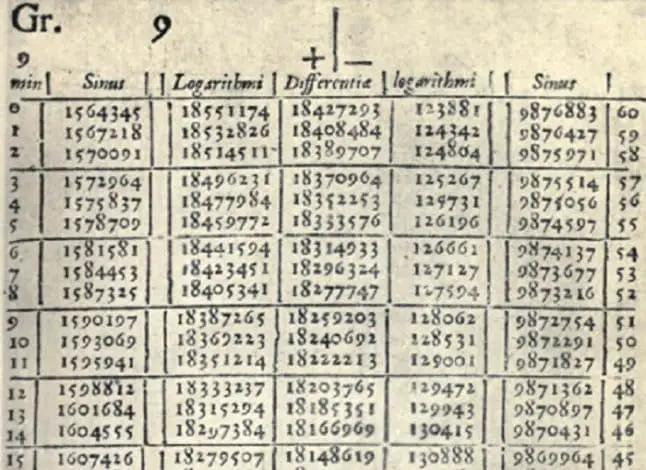
Napier bu kuralı uygulamak için art arda küçük zaman aralıklarında, noktaların ne kadar ilerleyeceğini yaklaşık olarak hesaplayan eşitsizlikler kurmuş ve ömrünün tam yirmi yılını bir logaritma tablosu
hazırlamakla geçirmiştir. Ancak gördüğünüz gibi Napier logaritması günümüzde kullandıklarımıza pek benzemez. Bunun için aradan biraz daha zaman geçmesi gerekecekti.
Doğal Ve Adi Logaritma Adı Nereden Geliyor?
Napier’in hesaplamalarını tamamlamasının ardından Oxford Üniversitesi’nde matematik profesörü olan Henry Briggs, Napier’in tablolarının önemini fark etti. Ancak bunların oldukça hantal olduğunu düşündü.
Napier logaritmasını temelinde üçgen çözümlemelerinde kullanılan denklemlerin çözümünü kolaylaştırmak için hazırlanmıştı. Tabloları bu tip sorularda işe yarıyordu. Ancak her zaman log(ab)=log(a)+log(b) eşitliğini sağlamıyordu. Devamında matematikçiler bu tabloları daha işlevsel hale getirme yarışına başlayacaklardı.
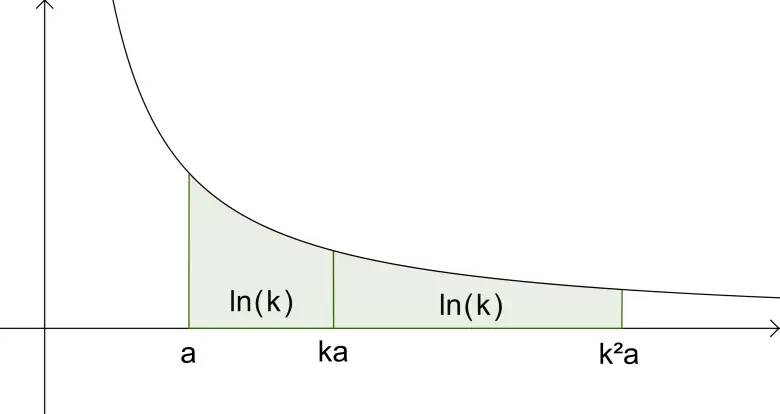
Bu süreçte işin içine adını bir çok kişinin duymadığı Gregory of Saint-Vincent (1584 – 1667) isimli bir başka matematikçi karışacaktı. Kendisi aslında bir hiperbol kolunun altındaki alanın özelliklerini inceliyordu. Yani aklında logaritmaya katkı sağlamak yoktu.
Çalışmasının bir noktasında Alan(ab)=Alan(a)+Alan(b) olduğunu gösterdi. Gregoire’ın bulduğu bu alan özelliği, logaritma fonksiyonunun özelliğinin tıpa tıp aynısıydı.
Yine de onun adıyla anıyor olmamız gereken logaritmaya doğal logaritma ya da Napier logaritması dendi. Bugün lnx biçiminde gösterdiğimiz bu logaritma aslında hiç de doğal olmayan bir biçimde Euler’in e sayısı kullanılır. Bu sayı yaklaşık 2,7182 gibi bir sayıdır. ( Detaylar: Euler Sayısı Diğer Adıyla e Sayısı Nedir ve Neden Önemlidir?)
Doğal denmesinin nedeni de bu logaritma fonksiyonunun kendine özgü davranış özelliklerinden dolayı, türev ve integral hesaplarında ve fiziksel olayların modellenmesinde karşımıza çıkmasıdır.
Hesaplamaya en uygun logaritma fonksiyonu ise 10 sayısını taban olarak kullanan logaritmadır. Bu logaritmaya da adi logaritma denir. Yaygın gösterimlerinden dolayı da bu 10 sayısı genelde yazılmaz. Herhangi bir hesap makinesindeki “log” ifadesi bu logaritmayı ifade eder.
Logaritma Nasıl Çalışır?
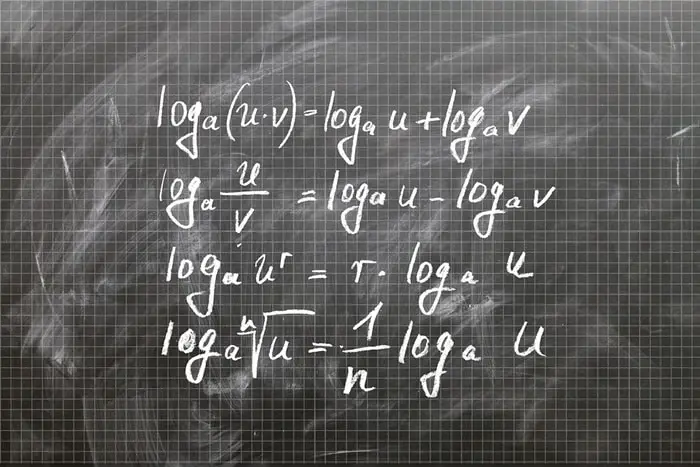
Herhangi bir hesap makinesinde log 1000 yazdığınızda 3 cevabını elde edersiniz. Bunun anlamı tabanımız 10 olduğu için 3 tane 10 sayısının çarpımının 1000 yapmasıdır. O zaman log 6’nın anlamı nedir diye düşünebilirsiniz.
10 sayısını kendisiyle belli bir sayıda çarpıp 6 elde edildiğini söylemek kulağa saçma gelir. Bu kavram elbette gerçek dünyada karşılığını bulmaz. Ama matematiğin gücü ve güzelliği buradan gelir. 6’nın logaritması, 0.778 sayısıdır. Başka bir deyişle, 10 sayısını kendisiyle 0.778 kere çarptığımızda 6’yı elde ederiz.
Şimdi gelin logaritma ile bir işlem yapalım. Örneğin 89 ile 62’yi çarpalım. Öncelikle logaritmalarını bulmamız gerekir ki günümüzde elimizin altındaki hesap makinaları yardımı ile bu oldukça kolay bir şeydir. Ancak 20. yüzyılın sonlarına kadar bunu yapabilmenin tek yolu logaritma tablolarından faydalanmaktı.
89’un logaritması 1.949’dur. 62’nin logaritması ise 1.792’dir. O halde logaritmalar toplamı 1.949 + 1.792 = 3.741 yapar. Logaritması 3.741 olan sayı ise 5518’dir. Bu da aynı şekilde logaritma tablolarından faydalanarak bulunur. O halde, 89 x 62 = 5518 ‘dir.
Logaritmaya Ne İşe Yarar? Günümüzde Halen İhtiyacımız Var mı?
Kısa cevap evet var. Günümüzde logaritma tabloları artık kullanılmasa da kendileri bilgisayarlarımızda var olmaya devam ediyor. Bilgisayarda sayıları çarpmak istediğimiz zamanlarda arka planda bir program çalışır. Bu programın sonuç verme süresi karmaşıklık ve hesaplama miktarı ile artar.
Saniyede milyonlarca sayının çarpılması gereken ve hızın kritik olduğu bir uygulamada bu bir sorun haline gelir. Bu nedenle bilgisayar belleğine bir program çalıştırmak yerine yalnızca değerleri araması gereken ve performansı artıran logaritma tabloları eklenir.
Logaritmaların bilimde birçok kullanımı vardır. Örneğin pH – bir çözeltinin ne kadar asidik veya bazik olduğunun ölçüsü – logaritmiktir. Depremlerle birlikte adını sık biçimde duyduğumuz Richter ölçeği de yine logaritmiktir.
Aslına bakarsanız üstel büyümenin olduğu hemen her yerde logaritma bir biçimde işe karışacaktır. Bu nedenle günümüzde tabloları kullanmaya gerek kalmasa da arka plandaki fikri bilmek hala gereklidir.
Kaynaklar ve ileri okumalar:
- How did Saint Vincent prove the logarithmic property of areas under hyperbolas?; Bağlantı: https://hsm.stackexchange.com/
- The making of the logarithm; yayınlanma tarihi: 14 mart 2014; bağlantı: https://plus.maths.org/content/dynamic-logarithms
Matematiksel