Kimisi için eğlence kimileri için de bir kaçış olan müzik, hayatımızın önemli bir parçasıdır. Ancak işin ilginç tarafı bir çok kişi müzikten keyif almasına rağmen matematikten kaçınmaktadır. Oysa ki tarih boyunca matematik ve müzik iç içe geçmiş ve pek çok matematikçi müzikle ilgilenmiştir.
Hatta Antik Yunan’da müzik, matematiğin 4 ana dalından biri olarak kabul edilmiştir. Gelin bu yazıda bazı tabuları yıkalım. Müziğin içindeki matematiği daha iyi anlamaya çalışalım. Ancak bunun için işe en başından başlayalım.
Ses Nedir?
Ses, bir nesne titreştiğinde oluşan bir dalgadır. Bir şey duyduğumuzda, ses dalgası titreşen nesneden aktarılır ve kulak zarımıza çarpar. Bu daha sonra beynimiz tarafından ses algısı olarak işlenir. Duyulan sesin kalitesi, ses dalgasının fiziksel özelliklerine bağlıdır.
Matematiksel bir açıdan baktığımızda da ses dediğimiz şey aslında sinüs dalgalarının bir karışımından oluşur. Ancak bir sesin parmak izini temelinde bazı şeyler belirler. Bunların en başında da frekans gelir.
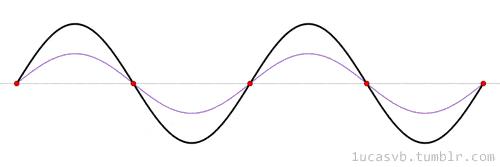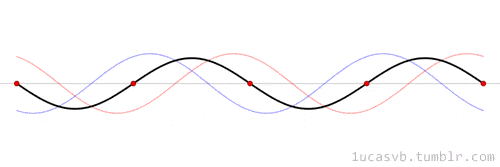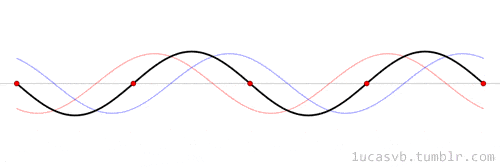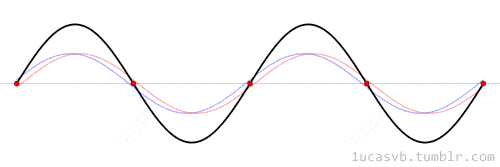
Dalgaların bir saniyede ileri geri gitme sayısı, o sesin frekansıdır. Ölçü birimi Hertz’dir. Yani 1 Hz, 1 saniyede 1 ileri-geri harekete eşittir. Sesin frekansı, sesin ne kadar yüksek veya alçak olduğunu belirleyen perdesini belirler. Daha yüksek frekanslı, yüksek perdeli bir ses, bir kara tahta üzerine sürten tırnak sesi gibidir. Daha düşük frekanslı, düşük perdeli bir ses ise bir bas davul sesi gibi olacaktır.
İnsan kulağı sınırlı miktarda frekans algılar. Bu sınır 20 Hz ile 20000 Hz arasında yer alır. Ses ile ilgili bilmeniz gereken bir başka önemli şey ise genliktir. Basitçe konuşmamız gerekirse, Genlik dalganın yüksekliğidir. Yükseklik, bir sesin şiddetini belirler. Sonucunda daha yüksek bir genlik, daha yüksek bir sesle sonuçlanır. Temel tanımları bir miktar anladıysak şimdi notalara geçebiliriz.
Notalar

Muhtemelen bir piyanonun tuşlarını görmüşsünüzdür. Her tuş bir notaya karşılık gelir ve benzersiz bir ses çıkarır. 7 beyaz anahtar ve 5 siyah anahtardan oluşan on iki tuştan oluşan sete bir oktav denir. On iki anahtar C’den A’ya düzenlenmiştir.
C1 32,70 Hz’de ve A1 55,00 Hz’de titrer. Bu notalar, frekanslarının artan sırasına göre düzenlenmiştir. Böylece, C1’den A1’e bir oktav olur. Bu oktavlar da sırasıyla C2’den A2’ye, C3’ten A3’e biçiminde de devam eder.
Matematik Ve Müzik İlişkisi
Bu noktadan itibaren matematik ve müzik ilişkisi daha da netleşecek. Sonucunda bir telin değişik boyları ile değişik sesler elde edildiğini ortaya çıkartan ilk kişi Pisagor‘dur. Pisagor, 12 birimlik bir teli ikiye bölmüş ve oktavı elde etmiştir. Elde edilen 6 birimlik uzunluk ( telin ½ si), 12 birimlik uzunluğun bir oktav tizidir.
Pisagor 8 birimlik uzunluk ile (telin 2/3 ü) 5 li aralığı, 9 birimlik uzunluk ile (telin ¾ ü) 4 lü aralığı bulmuştur. Esas sesimiz “do” olsun. Do sesinin ½ si bize onun bir oktav tizini, 2/3 ü sol sesini, ¾ ü fa sesini, 8/9 i ise “re” sesini, 64/81 i ise mi sesini vermektedir.
Bu şekilde gidildiği zaman; Do, re, mi, fa, sol, la, si, do sesleri sırasıyla; 1, 8/9, 64/81, 3/4, 2/3, 16/27, 128/243 ve 1/2 oranları ile ifade edilir. Gördüğününüz gibi notalar biçiminde düşündüğümüz şey temelinde bir matematiksel dizi oluşturmaktadır.
Pisagor; “Tellerin kıpırtısında geometri vardır, küreler arasındaki boşlukların hesaplanmasında da müzik” deyişi ile de düşüncesini bir adım öteye taşıdı. Çünkü cümlede adı geçen küreler gökcisimleri idi. Böylece Kürelerin müziği veya diğer adıyla kürelerin armonisi kavramı ortaya çıkacaktı. ( Daha fazlası için: Müzik İle Evrenin Uyumu: Kürelerin Müziği)

Buraya kadar aktardıklarımız neticesinde sizin de fark ettiğiniz gibi temelinde müzik ve matematik başlangıçta içiçe geçmiş durumdaydı. Ancak sonrasında bir biçimde birbirinden ayrıldı, ya da deneyimsiz gözler ayrıldığını düşündü.
Konumuza geri dönelim. Şu ana kadar gördüğümüz bilgilerin hepsi her enstrüman için geçerlidir. Ancak, bu noktada hala aktarmadığımız bir bilgi var. Sonucunda ortak kavramlar üzerine yapılanmış olmasına rağmen enstrümanlar neden farklı sesler çıkarıyorlar?
Bir tele bastığınızda her zaman belirli bir müzikal perdeye sahip bir ses duyarsınız. Müzisyenlerin bildiği gibi bir telin uzunluğu, gerilimi veya ağırlığı değiştirilerek perde değiştirilebilir. Bir tencereye veya masaya çarpma sesiyle karşılaştırıldığında bu telin özelliği nedir? Ya da bir davulda duyduğumuz do sesi ile bir piyanoda duyduğumuz arasında ne fark vardır?
Farklı enstrümanlardan aynı notayı çaldığımızda farklı duymamıza sebep olan şey nedir?
Yukarıdaki soruların cevabını anlamak için frekans kavramına geri dönmemiz gerekiyor. Telin ağırlığı, gerilimi ve uzunluğu seçilerek en düşük frekans sabitlendikten sonra, diğer tüm frekanslar bu frekansın tamsayı katları biçiminde olur. Yani eğer birinci frekans f ise, ikincisi 2f, üçüncüsü ise 3f biçiminde olacaktır.
Bu frekanslara doğal frekanslar ( overtones) denir. Onları ilişkilendiren bu basit sayısal modele harmonik seri ( matematikteki harmonik seriler ile karıştırmayalım) denir. Her doğal frekans, belirli bir titreşim modeliyle ilişkilendirilir.
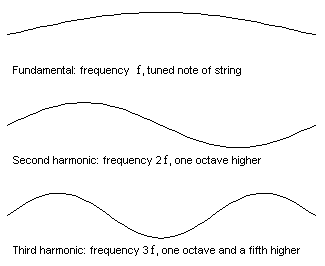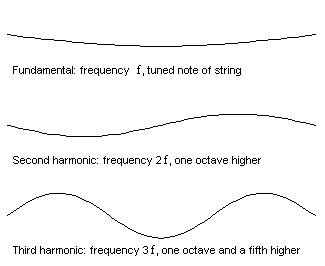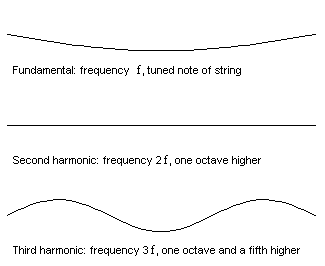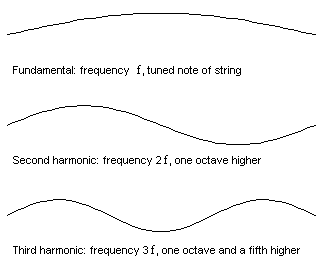
Aynı frekansı taşıyan bir notanın her enstrümanda aynı sesi çıkarmamasının nedenlerinden biri de budur. Örneğin A3 notasını çaldığımızda (110 Hz) duyduğumuz ses tek bir frekanstan oluşmaz. Ses, temel frekansın (A3) altında gizli frekanslar içerir. Tel 110 Hz’de bir kez, 220 Hz’de iki kez ve 330 Hz’de üç kez titreşir. Sonucunda bu eşzamanlı olarak gerçekleştiği için gitarın benzersiz sesi ortaya çıkar.
Ancak aynı benzersiz titreşim her enstrümanda karşımıza çıkmayacaktır. Akortlu bir vurmalı çalgı yapma sanatı ve bilimi, tamamen doğal frekansları veya en azından birkaçını armonik ilişkilere dönüştürmekle ilgilidir.
Sesin Tınısı Nedir?
Bir sese ayırıcı adını veren frekans, aslında, o sesle aynı anda tınlayan farklı seslere temel oluşturan en kalın sese aittir. Temel sesin üzerinde tınlayan bu seslere armonikler denir. Kulaklarımız farklı sesleri algılamakta çok iyidir. Bunu yapmanın bir yolu sesin “tınısı” dır. Tını, sesin ton kalitesi veya ton rengidir. Sesin tınısı, sesin yaptığı armoniklerle belirlenir. Her armonikteki genlik ve perde değişikliği, enstrümanlara kendi tınılarını verir.
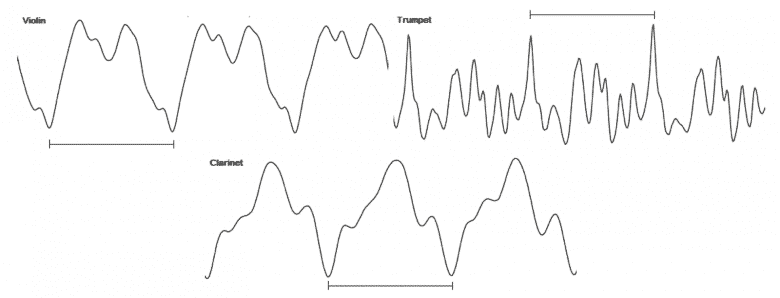
Bir enstrümanın tınısını doğrudan etkilediği için, enstrümanların materyali de farklılaşmış seslerinin ana nedenlerinden biridir. Farklı malzemeler sesin hızını etkileyen farklı yoğunluklara sahiptir. Bazı malzemeler sesi daha çok yansıtır ve bu da bir sese daha fazla katman ekler. Malzemelerin titreşimleri de dikkate alınması gereken bir faktördür. Metal, plastikten farklı titreşir ve daha net bir ses verir.
Sonuç olarak ses, insan deneyiminin önemli bir parçası olan, doğanın temel güçlerinden biridir. Özetle aktarmaya çalıştığımız gibi de müzik arka planda önemli bir oranda matematik ve fizik barındırır.
Matematik ve müzik ilişkisini aktarmaya çalıştığımız bir yazı Fourier dönüşümünden bahsetmez ise bir miktar eksik kalır. Ancak konuyu fazla uzatmak istemedik. Dilerseniz bu yazımızda detaylara göz atabilirsiniz: Fourier Dönüşümü: Basit Bir Formül Dünyayı Nasıl Değiştirdi?. Hayatınızdan hem müziği hem de matematiği eksik etmemeniz dileğimizle.
Kaynak ve ileri okumalar:
- Why Do Different Musical Instruments Make Different Sounds?; https://www.scienceabc.com/
- Maths in a minute: Maths and music; yayınlanma tarihi: 2 Kasım 2021; Bağlantı: https://plus.maths.org/
- What makes an object into a musical instrument?. Yayınlanma tarihi: 3 Şubat 2011; Bağlantı: https://plus.maths.org/content/what-makes-object-musical
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel