Bir matematik problemini güzel yapan şeylerden birisi, onu çözmeye çalışırken bazı beklenmedik keşifler yapma potansiyelinizin olmasıdır. En azından Esther Klein’ın 1933’teki deneyimi böyleydi. Üstelik bu keşif beklenmedik bir biçimde mutlu bir sonla bittiği için matematikte önemli bir probleme de adını verecekti.
O sırada Klein 23 yaşındaydı ve memleketi Budapeşte, Macaristan’da yaşıyordu. Bir gün iki arkadaşı Paul Erdős ve George Szekeres kendisine bir bulmaca getirdi. Sonra üçlü bu bulmacayla uğraşmaya başladı.
İşte bu bulmacaya ilerleyen süreçte, matematikle hiçbir ilgisi olmayan nedenlerle, Paul Erdős tarafından mutlu son problemi adı verildi. Bunun nedeni de Esther Klein ve George Szekeres’in problemle uğraşırken birbirlerine aşık olmaları ve 13 Haziran 1937’de evlenmeleriydi.
Mutlu Son Problemi Nedir?
Bu problem açıklaması oldukça kolay ancak tüm cevaplama girişimlerine meydan okuyan matematiksel sorulardan biridir. Konu oldukça basittir çünkü temelinde bir kağıda çizilen noktalar ve bunları birbirine bağlayarak oluşturabileceğiniz şekillerle ilgilidir. Ancak basit görüntüsü aldatıcıdır. Dünyanın en iyi matematikçilerinden bazıları konu üzerinde uzun zaman boyunca çalışmalarına rağmen sonuca ulaşamamışlardır.
Bir kağıda çizilmiş, hepsi düz bir çizgi üzerinde yer almayan yani doğrusal olmayan üç noktanız olsun. Bu üç noktayı köşeler olarak kabul ederseniz bir üçgen çizebilirsiniz. Elinizde dört nokta olduğunda da (üç tanesi aynı çizgide olmayan) bunları birleştirerek dört kenarlı bir şekil çizebilirsiniz.
Ancak noktaların nasıl dağıldığına bağlı olarak, bazı dörtgenler biraz tuhaf görünecektir. Aşağıdaki görselde ortada yer alan çokgen içbükey ve yanlardakiler ise dışbükeydir. Aslında sizin de fark etmiş olacağınız gibi dört nokta verildiğinde, bunları bir dışbükey dörtgen oluşturacak şekilde birleştirmek her zaman mümkün değildir.
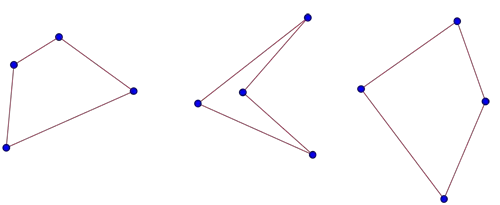
Farz edelim ki elinizde 5 tane nokta var ve bu noktaları bir kağıdın üzerine rastgele (herhangi üçü aynı çizgide olmamak kaydıyla) yerleştirdiniz. Şimdi bu noktaların dördünü kullanarak dışbükey dörtgen çizmeye çalışın.
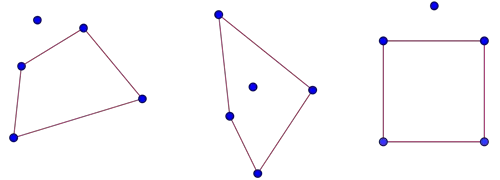
Aslında bu fazladan bir nokta size bunu yapmak için esneklik sağlayacaktır. 5 nokta ile her zaman bir dışbükey dörtgen çizebilirsiniz. Aşağıda bazı örnekler görebilirsiniz.
Elimizde Daha Fazla Nokta Olduğunda Durum Ne Olacak?
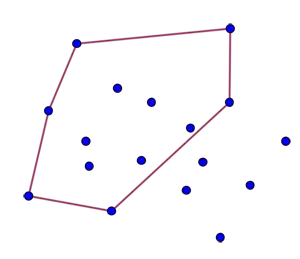
Herhangi üçü doğrusal olmayan dokuz nokta yardımıyla bir beşgen elde etmeniz de garantidir. Aynı mantıkla 17 nokta kullanarak noktaları nasıl yerleştirirseniz yerleştirin kesin bir dışbükey altıgen yaratabilirsiniz.
O zaman sorumuzu soralım. Bir dışbükey n-gen çizmek için kaç en az kaç noktaya ihtiyacımız var? Mesela bir dışbükey yedigen çizebildiğinizden emin olmak için size kaç nokta gerekiyor? Aslına bakarsanız bunu kimse bilmiyor. Aynı şekilde 8, 9, 10 için de bilmiyoruz.
Mutlu Son Problemi Nasıl Çözüldü?
1935’te Erdős ve Szekeres bu sorunu üç, dört ve beş kenarlı şekiller için çözmüştü. Erdős ve Szekeres, bu çözümlerini sundukları makalede, herhangi bir sayıda kenardan oluşan bir dışbükey çokgeni çizmeyi garanti etmek için gereken nokta sayısı için de bir formül önermişlerdi. Erdős ayrıca bu formülün doğru olduğunu kanıtlayabilen herkese 500 dolarlık ödül vereceğini de söylemişti. ( Bu ilginç matematikçiyi tanımak isterseniz: Paul Erdös: Kahveyi Teoreme Dönüştüren Büyük Yaşlı Adam)
Formül 2(n–2) + 1 biçimindeydi. Formülde n kenar sayısı anlamına geliyor. Buna göre şu ana kadar elde ettiğimiz sonuçların bu denklemde denemesi aşağıdadır.
- n=3 için 1+2n-2=1+23-2= 3
- n=4 için 1+2n-2=1+24-2= 5
- n=5 için 1+2n-2=1+25-2= 9
- n=6 için 1+2n-2=1+26-2= 17 şeklinde olacaktır.
Ancak bunun doğru olup olmadığını 6’dan büyük sayılar için bilemiyoruz. Yeterince nokta çizerseniz bu noktaların bazılarını köşe olarak kabul eden n kenarlı bir dışbükey çokgen olacağından emin olabilirsiniz. Burada kanıtlanamayan şey yeterince dediğimiz nokta sayısıdır.
Erdős ve Szekeres formüllerini kanıtlayamadılar, ancak bir matematikçinin oraya ulaşmak için izleyebileceği yolu net bir şekilde anladılar. Bunun sonucunda da formülün doğru olup olmadığını kanıtlamak için matematikçiler uzun süre çalıştılar.
Geçtiğimiz yıllarda Chicago, Illinois Üniversitesi’nden Andrew Suk, 80 yılı aşkın bir süre önce Erdős ve Szekeres’e rehberlik eden sezginin doğru olduğuna dair neredeyse kesin kanıtlar sundu. Bugün bu üçlünün hiçbiri aramızda olmasa da problem çözüme çok yaklaştı.
Sonuç Olarak;
Mutlu son problemi ilginç bir fenomeni ortaya çıkarır. Eğer bir sistem yeterince büyükse (örneğin yeterince çok nokta), o zaman sistem bir bütün olarak düzensiz olsa bile, içinde bir miktar düzen (örneğin dışbükey şekiller) bulmayı umabilirsiniz. Bu durum da Ramsey teorisi adı verilen bir matematik alanı tarafından incelenir.
Kaynaklar ve İleri Okumalar:
- Happy Ending Problem – Numberphile; https://www.youtube.com/
- Happy ending problem; https://en.wikipedia.org/wiki/Happy_ending_problem
- A Puzzle of Clever Connections Nears a Happy End. Yayınlanma tarihi: 30 Mayıs 2017; Bağlantı: https://www.quantamagazine.org/a
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
