Odanızın duvarına asılı duran Escher posterinin matematikle sandığınızdan daha fazla bağlantısı var. Escher’in çizimleri, şekillerin üst üste binmemesi ve aralarında boşluk kalmaması için iki boyutlu bir düzlemin geometrik şekillerle kaplanması anlamına gelen tessellation diğer bir değişle mozaikleme yani bir düzlemin belirli bir şekille kaplanması örnekleridir.
Bir düzlemi eşkenar üçgen, kare ve altıgen ile kolayca kaplamak mümkündür. Ancak Escher’in çizimlerinin de kanıtladığı gibi, bu şekillerin üçgen veya kare olması gerekmez. İsterseniz kuşlar, melekler, balıklar veya damlalar gibi şeylerle de bir düzlemi kaplayabilirsiniz.

Aslında, bir yapboz bulmacayı da bir tür mozaik ile kaplama örneği olarak düşünebilirsiniz. Parçalar bu bulmacada da üst üste binme ve boşluk olmadan tamamen doldurmak için birbirine uyum sağlamaktadır.
Ancak mozaikler yalnızca Escher posterlerinde veya bulmacalarda bulunmaz. İspanya’da bulunan Alhambra sarayının karmaşık duvar süslemelerinde, bir bal peteğindeki altı kenarlı hücrelerde, antik Roma binalarındaki duvarları ve zeminleri kaplayan geometrik desenlerde, yorganlardaki şekillerde, mozaikler her yerdedir.
Zaman içinde yapılan çalışmalar sonucunda matematikçiler mozaiklerin belirli şekillerde meydana geldiğini keşfetmişlerdir. Bazı mozaikler periyodiktir yani kalıplar tekrar eder. Bazıları ise periyodik değildir ve bunların içinde tekrar eden kalıp yoktur.

Periyodik kaplamalar, sadece çokgensel bölgelerden biriyle yalnız öteleme dönüşümü kullanılarak düzlemde boşluk kalmayacak ve çakışmayacak şekilde düzlemin örtülmesidir. Yürürken basıp geçtiğimiz kaldırımlar buna en basit verilecek örnektir. Kısacası periyodik kaplamalarda aynı şekil tekrar eder durur. Bu nedenle düzlemi doldurmak oldukça kolaydır.
Bir Düzlemi Neden Beşgen İle Kaplayamıyoruz?
Dikkat ettiyseniz, düzenli çokgenlerle yapılan döşemelerde, beş sayısı bariz bir şekilde yoktur. Bunun neden olmadığını aslında anlamak kolaydır. Sonuçta düzgün bir beşgenin beş iç açısı 108 derecedir.
Beşgenleri bir noktanın etrafına yerleştirmeye çalışırsak aralarında boşluk kalacaktır. Çünkü 3 × 108 = 324 yapar ki bu 360 dereceden küçüktür. 4 tane beşgen koyarsak da beşgenler üst üste gelir. Bu seferde 4 × 108 = 432 derece yapar bu da 360 dereceden büyüktür.
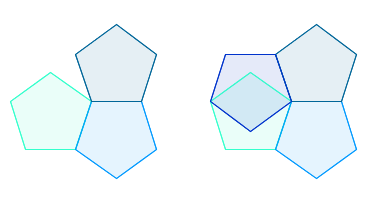
Ancak pes etmeye gerek yok. Düzenli döşemelerdeki bazı kısıtlamaları kaldırırsak belki de beşgenleri bir düzlemi kaplamada kullanabiliriz. Şimdi kullandığımız her bir çokgenin birbirinin aynısı olması kuralını unutalım. Tek şartımız her bir döşemenin beş katlı dönme simetrisine sahip olmasını olsun.
( Bir şekil kendi etrafında 360 derece döndürüldüğünde yine kendisi ile çakışır. Bazı şekiller ise 360 dereceden daha küçük açı ile döndürüldüğünde yine kendisi ile çakışır. Böyle şekiller dönme simetrisine sahiptir.)
Şimdi düzlemi döşeyecek beş katlı dönme simetrisine sahip bir dizi şekil bulmak mümkün mü? Bu soru kolayca ifade edilse de, çözümü oldukça zordur. Soru aynı zamanda, birçok harika geometrik tasarımın kaynağıdır.
Kuralları Biraz Esnetelim!
Şimdilik, böyle bir döşemenin neden var olup olmaması gerektiğine dair matematiksel bir açıklamaya girmeyelim. Kendimiz oluşturmaya çalışalım. İşe beş katlı dönme simetrisine sahip olduğunu bildiğimiz düzgün çokgen ile başlayalım.
Bu şeklin 5 kenarının her birine bir beşgen daha ekleyebiliriz. Ancak bu durumda beşgenler arasında 36 derece boşluk kalır. Şimdi bu boşlukları beş katlı dönme simetrisine sahip olduğunu bildiğimiz bir başka şekille, 5 köşeli yıldız ile dolduralım.
Beş köşeli yıldızlardan geriye kalan boşlukları da daha evvel kullandığımızın iki katı büyüklüğündeki beşgenler ile yine dolduralım. Şeklimiz burada sona erdi. Çünkü aşağıdaki görselde de göreceğiniz gibi artık yeni bir yıldız ekleyemiyoruz.
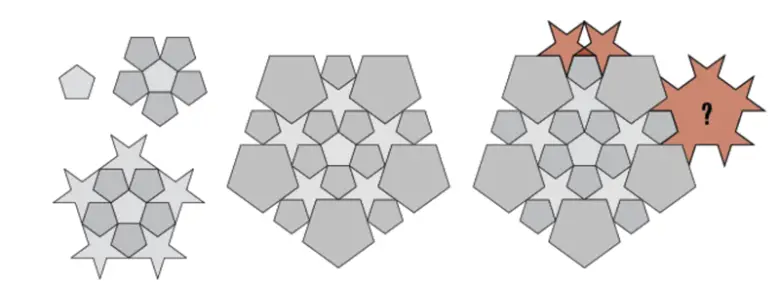
Belki de yukarıda yanlış bir başlangıç yaptık diye düşünebilirsiniz. Yani en başta ortaya beş köşeli bir yıldız yerleştirip, gerekli yerlere beşgenler ekleyerek şekli inşa etmeye baştan başlayabilirsiniz. Ancak eninde sonunda yine tıkanacaksınız. (Denemesi ödev olsun).
Demek ki beş katlı dönme simetrisine sahip olmayan bazı ek şekilleri kabul etmemiz gerekiyor. Gerçekten de fazladan şekillere izin vermek sorunu çok kolaylaştırır. Bir eşkenar dörtgen ve iki düzgün beşgenin oluşturduğu sekizgen bir bölge düzlemi döşer.
Aslında, düzlemi bu iki şekille döşemek için sonsuz sayıda yol vardır. Hatta merkezde bir ongen ile işe başlarsanız şekilde sağda gösterildiği gibi çekici bir spiral düzen de oluşturabiliriz.
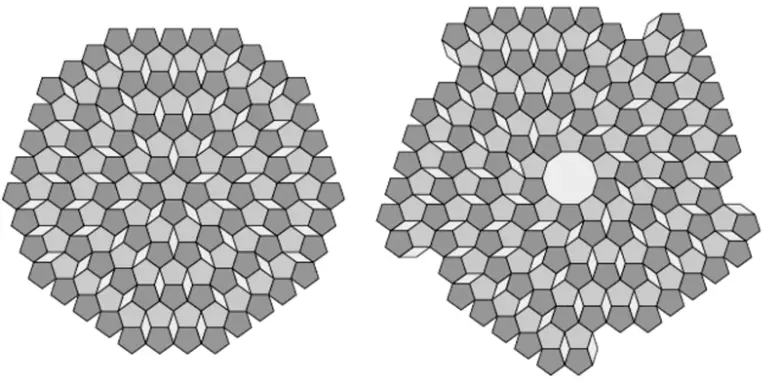
Şimdi ortaya başka bir soru çıktı. Beş katlı dönme simetrisine sahip olmayan eşkenar dörtgen gibi şekillere izin verdikten sonra, onları daha uygun parçalara bölebilir miyiz? Bu soru bizi döşeme teorisindeki önemli bir kavrama götürür. Bu kural sayesinde bir beşgen ve eşkenar dörtgen aşağıdaki biçimde bölünmektedir. Bu sayede de daha önceden üretemediğimiz şekilleri oluşturmamız mümkün olur.
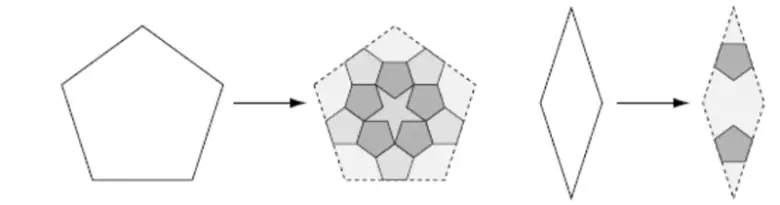
Penrose Karoları Nedir?
Yukarıda kısaca aktardığımız parçalama sürecine benzer bir yöntem yirminci yüzyılda Sir Roger Penrose tarafından tasarlandı ve şaşırtıcı yeni bir keşfe yol açtı. Şu ana kadar periyodik mozaikler ile uğraştık. Ancak modelin tekrar etmediği periyodik olmayan mozaikleri bulmak daha zordur.
Uzun zaman boyunca periyodik olmayan parçaların var olmadığına inanılmıştı. Penrose beşli dönme simetrisine sahip (pentapleks) karolarla bir düzlemi kaplayan, ama kendini tekrarlamayan yani periyodik olmayan kaplamalar yapmayı başarmıştı.

En basit şekliyle anlatmak gerekirse yaptığı şey, eşkenar dörtgeni adlarına ok ve uçurtma dediği iki farklı şekil elde edilecek biçimde ikiye bölmekti. Sonrasında yapması gereken bu şekillerin bir araya gelerek oluşturdukları desenleri periyodik olmasını kısıtlayacak bir biçimde nasıl birleşebileceğine dair bir kural formüle etmekti. Bunu her uçurtma ve okun üzerine bir yay çizerek ve yayların daima benzerleriyle birleştirilmesini şart koşarak yaptı.
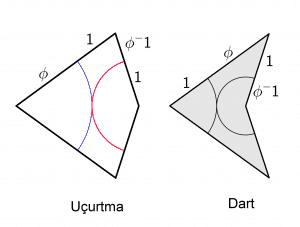
Periyodik olmayan parçaların birleştirilebilmesi matematik için heyecan verici bir kırılma noktasıydı. Ancak bu çalışmanın asıl faydası fizik ve kimyada yapılan bir buluş ile anlaşıldı. 1980’li yıllarda araştırmacılar var olduğuna inanmadıkları bir kristal keşfettiler.
Bu küçük yapı periyodik olmayan bir desen sergiliyordu ve Penrose’un iki boyutlu yapısının üç boyutlu halini sergiliyordu. Bu yapıların varlığı -kristalimsiler- bilim insanlarının madde anlayışlarını değiştirdi. Tüm kristallerin platonik katılardan çıkarılan simetrik örgüye sahip olmaları gerektiği yönündeki klasik görüşü ortadan kaldırdı.
Güncelleme:
Penrose karolarının devamında matematikçilerin konu ile ilgili arayışları devam etti. Amaç aslında periyodik olmayan tek bir çokgen elde edebilmekti. Sonunda 20 Mart 2023 tarihinde amaçlarına ulaştılar. Aşağıda yeni keşfedilen 13 kenarlı periyodik olmayan bu şekli görüyorsunuz.

İyi de bu benim ne işime yarayacak ki? derseniz. Unutmayalım, tekrarlanmayan döşemeler oluşturan şekiller, daha güçlü malzemeler tasarlamaya yardımcı olacaktır. Ayrıca göz atmak isterseniz: Göz atmak isterseniz: İki İmkansız Şekil Tanıyalım: Penrose Üçgeni Ve Penrose Merdiveni
Kaynaklar ve ileri okumalar:
- The trouble with five; Yayınlanma tarihi: 1 Kasım 2007; Bağlantı: https://plus.maths.org/
- At Long Last, Mathematicians Have Found a Shape With a Pattern That Never Repeats. yayınlanma tarihi: 29 Mart 2023; bağlantı: https://www.smithsonianmag.com/
Matematiksel