
Matematiksel denklemler sadece faydalı olmakla kalmaz. Konu ile ilgili olmayanlar fazla fark etmese de aslında birçoğu oldukça güzeldir. En azından matematikçiler ve bilim insanları böyle düşünüyor. Geçtiğimiz yıllarda fizikçilere, astronomlara ve matematikçilere en sevdikleri, onlara göre en güzel denklemler soruldu. Verdikleri cevaplara göz atalım.
Genel görelilik
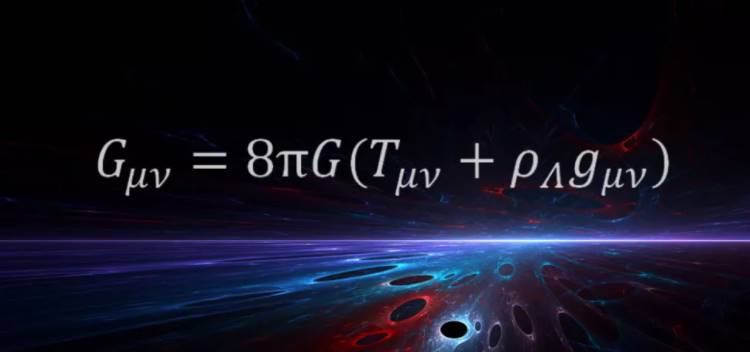
Yukarıdaki denklem Einstein tarafından 1915’te çığır açan genel görelilik teorisinin bir parçası olarak formüle edildi. Denklemi favorisi olarak gösteren astrofizikçi Mario Livio’ya göre, bu denklem uzay-zamanın neyle ilgili olduğunu açıklama potansiyeline sahip. Bu nedenle Einstein’ın tüm gerçek dehası bu denklemde vücut buluyor.
Denklemin sağ tarafı, evrenimizin enerji içeriğini (mevcut kozmik ivmeyi harekete geçiren ‘karanlık enerji’ dahil) tanımlıyor. Sol taraf ise uzay-zamanın geometrisini tanımlıyor. Yani denklem, uzay-zaman, madde ve enerji arasındaki ilişkiyi ortaya çıkarıyor. Einstein’ın Genel Görelilik Teorisi bize uzayın (ve zamanın) eğrilebileceğini söylüyor. Bu denklem, Newton’un öngörülerinin gerçekleri tam olarak yansıtmadığını göstermesi bakımından çok büyük öneme sahiptir.
Standart Model

Fiziğin hüküm süren teorilerinden bir diğeri de standart modeldir. Bu denklem şu anda evrenimizi oluşturduğu düşünülen temel parçacıkların birleşimini tanımlar. Bu denklemi favorisi olarak gösteren fizikçi Lance Dixon’a göre denklem, laboratuvarda (ve günlük yaşantılarımızda) bugüne kadar gözlenmiş bütün parçacıkların ve kuvvetlerin tanımını yapabilmektedir.
Denklem, kuantum mekaniği ve özel görelilik teorisi ile tamamen uyumludur ve onları içerisinde barındırmaktadır. Bununla birlikte, standart model teorisi henüz genel görelilik ile birleştirilmemiştir, bu yüzden yerçekimini tanımlayamaz.
Kalkülüs’ün Temel Teoremi
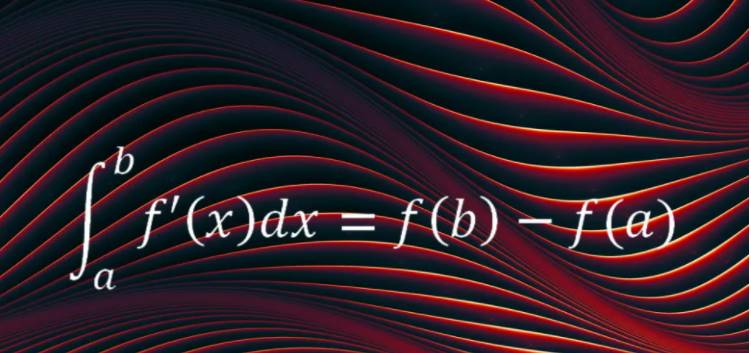
İlk iki denklem evrenimizin belirli yönlerini tanımlar. Ancak, başka bir favori denklem her türlü duruma uygulanma potansiyeline sahiptir. Kalkülüs’ün temel teoremi, kalkülüs yani analiz olarak bilinen matematiksel yöntemin omurgasını oluşturur.
Bu teorem iki ana fikri, integral kavramını ve türev kavramını birbirine bağlar. ( Detaylar için: Türev Nedir? İntegral Nedir?). Fordham Üniversitesi matematik bölümü başkanı Melkana Brakalova-Trevithick’, bu denklemi favorisi olarak seçmiştir.’ göre bu denklem en güzel denklem kabul edilmelidir.
Pisagor Teoremi

Hepimizin yakından tanıdığı Pisagor teoremi matematikçilerin hala gözdesi. Bu formül, herhangi bir dik üçgen için hipotenüsün uzunluğunun karesinin (c) (bir dik üçgenin en uzun kenarı) diğer iki kenarın (a ve b) uzunluklarının karelerinin toplamına nasıl eşit olduğunu açıklar.
Pisagor teoremi hakkında daha fazla detay için bu yazımıza bakmalısınız. Bu arada bu teoremi bunca seçenek arasında hala ilk sıraya koyan kişi Cornell Üniversitesi’nden matematikçi Daina Taimina oldu.
Özel Görelilik
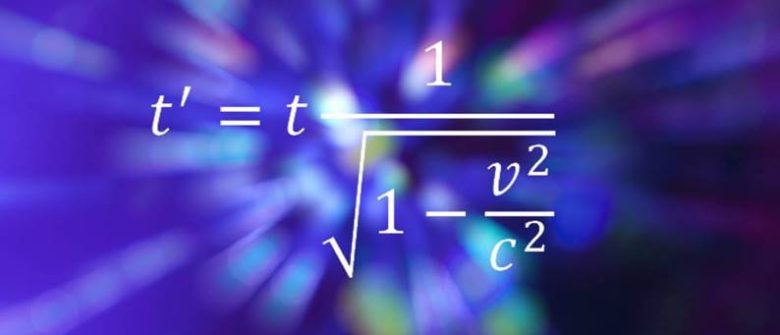
Einstein, zaman ve uzayın mutlak değil, gözlemcinin hızına bağlı olarak göreceli kavramlar olduğunu açıklayan özel görelilik formülleriyle listeyi yeniden giriş yapıyor. Einstein’ın özel görelilik üzerine ünlü makalesi cisimlerin hareketleriyle ilgili düşüncelerimizde devrim yaratmıştır. Bu sayede, bir zamanlar mükemmel kabul edilen Newton’un klasik kuramını özel bir duruma indirgemiştir.
Bu denklemi favorisi seçen parçacık fizikçisi olan Bill Murray’e göre denklem, dünyaya bakmanın yepyeni bir yolunu gösterir. Sonuçta ortada artık katı gerçekler yoktur. Ancak bunun yerine gözlemlediğiniz şeyle ilgili değişen olgular vardır.
Denklemde “v”, bir cismin hızını, “c” ışık hızı sabitini, “t” referans düzlemindeki zamana, t’ ise gözlemci tarafından deneyimlenen zaman anlamına gelir. Buna göre, gözlemcinin hızı ışık hızına yaklaştıkça, zaman onun için yavaşlar ve ışık hızına ulaşıldığında tamamen durur.
Euler Çokyüzlü Formülü

Massachusetts’teki Williams Koleji’nde matematikçi olan Colin Adams’ın tercihi olan bu formül, bir çokyüzlünün köşe sayısını V, kenar sayısını E ve yüz sayısını F ile gösterirsek, bu üç nicelik arasındaki ilişkiyi tarif eder.
Denkleme göre, yüz sayısı ile köşe sayısının toplamından kenar sayısını çıkarırsanız, hangi şekli inceliyor olursanız olun 2 sayısını elde edersiniz. Örneğin, dört üçgen, altı kenar ve dört köşeden oluşan bir tetrahedron düşünelim. Esnek yüzleri olan böyle bir dörtyüzlüye sert bir şekilde üflerseniz, onu bir küre haline getirebilirsiniz. Bu sayede bir küre dört yüze, altı kenara ve dört köşeye bölünür. Bu formül sayesinde topolojide önemli çalışmalar yapılmaktadır.
Euler-Lagrange Denklemleri ve Noether Teoremi
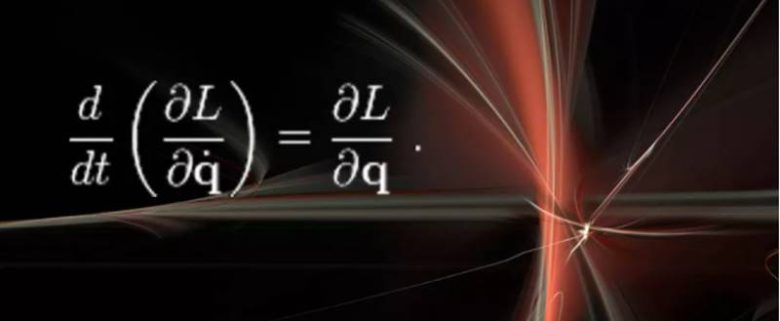
Denklemdeki L yaylar, kaldıraçlar veya temel parçacıklar gibi fiziksel bir sistemdeki enerjinin bir ölçüsü olan Lagrange’ı temsil eder. Bu denklemi çözmek size sistemin zamanla nasıl gelişeceğini söyler. Lagrange denkleminin bir yan ürünü, 20. yüzyıl Alman matematikçisi Emmy Noether’den sonra Noether teoremi olarak adlandırılır.
Bu teorem kabaca, sisteminizin bir simetrisi varsa, buna karşılık gelen bir korunum yasası vardır der. Yani, fiziksel bir sistemdeki simetrileri ve koruma yasalarını ilişkilendirir. Örneğin, fiziğin temel yasalarının bugün ve yarın aynı olduğu fikri (zaman simetrisi) enerjinin korunduğunu ima eder.
Fizik yasalarının uzayda olduğu gibi Dünya’da da aynı olduğu fikri nedeniyle momentum korunur. Bunlar oldukça soyut ama bir o kadar da önemli bulgulardır. Emmy’nin çalışmasının bir bölümünü, genel göreliliğin bazı bölümlerini formüle etmek üzere Einstein kullanmıştır. Detaylar için: Fizikte Simetri ve Korunum Yasaları Üzerine Kısa Bir Bakış
Callan-Symanzik Denklemi
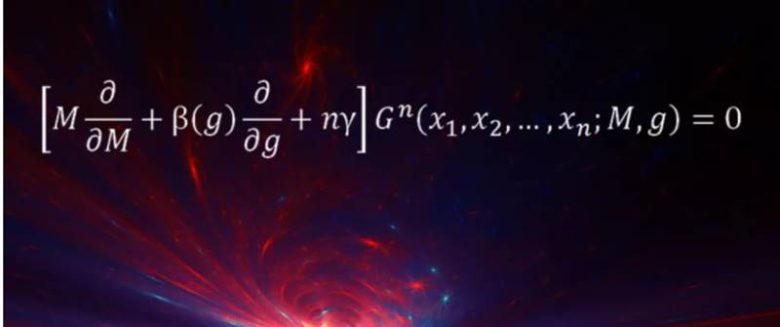
Rutgers Üniversitesi’nden teorik fizikçi Matt Strassler, “Callan-Symanzik denklemi, kuantum dünyasında saf beklentilerin nasıl başarısız olacağını açıklamak için gerekli olan, 1970’den kalma hayati bir ilk ilkeler denklemidir” diyor.
Denklemin, fizikçilerin atom çekirdeğini oluşturan proton ve nötronun kütlesini ve boyutunu tahmin etmelerine izin vermek de dahil olmak üzere çok sayıda uygulaması vardır. Temel fizik bize iki nesne arasındaki yerçekimi kuvvetinin ve elektrik kuvvetinin, aralarındaki mesafenin karesinin tersiyle orantılı olduğunu söyler.
Aynı şey, atomların çekirdeğini oluşturmak üzere protonları ve nötronları birbirine bağlayan ve protonlar ile nötronları oluşturmak üzere kuarkları birbirine bağlayan güçlü nükleer kuvvet için de geçerlidir.
Bununla birlikte, küçük kuantum dalgalanmaları, bir kuvvetin mesafeye bağımlılığını hafifçe değiştirir. Bu, güçlü nükleer kuvvet için dramatik sonuçlar doğurur. Callan-Symanzik denkleminin yaptığı şey, [mesafe] kabaca bir proton boyutunda olduğunda ölçülebilen, hesaplanması daha kolay bir biçime çevirmektir.
Euler Doğrusu
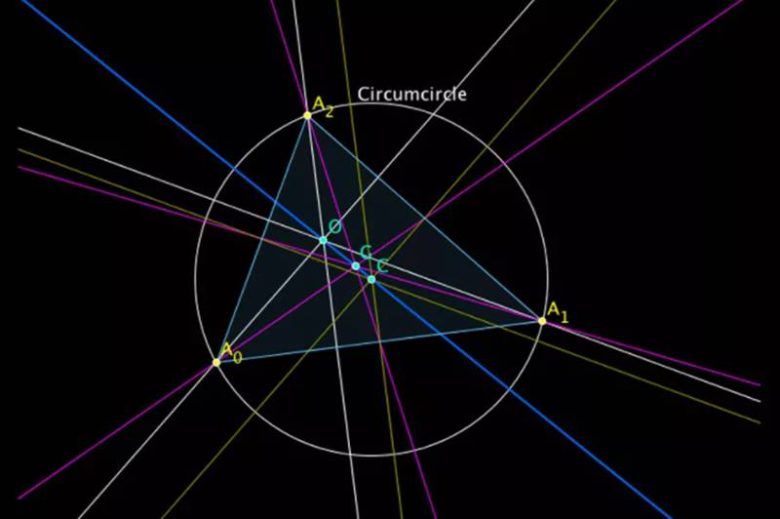
New York’taki Matematik Müzesi’nin kurucusu Glen Whitney, başka bir geometrik teorem seçti; bu teorem, adını 18. yüzyıl İsviçreli matematikçi ve fizikçi Leonhard Euler’den alan Euler doğrusu ile ilgiliydi. Herhangi bir üçgenle başlayın.
Üçgeni içeren en küçük daireyi çizin ve merkezini bulun. Üçgenin ağırlık merkezini bulun. Şimdi de üçgenin üç yüksekliğini çizin ve hepsinin birleştiği noktayı bulun. Teorem, az önce bulduğunuz üç noktanın her zaman tek bir düz çizgi üzerinde uzanmasıdır.
1 = 0.999999999…

0.999…biçimde devam eden bir sayının bire eşit olduğunu belirten bu basit denklem, Cornell Üniversitesi’nden matematikçi Steven Strogatz’ın favorisidir. Kendisi bu denklemi basit ama kışkırtıcı olarak nitelendiriyor. Ona göre sol taraf matematiğin başlangıcını temsil ediyor. Sağ taraf ise sonsuzluğun gizemini barındırıyor. Ayrıca göz atmak isterseniz: 0.99999…=1, Bu Sonuçtan Gerçekten de Emin miyiz?
Sizin için en güzel denklem hangisi? Bunu yorumlara ekleyebilirsiniz. Ayrıca bu yazımıza da bakabilirsiniz: Dünyayı Değiştiren Günümüzü Biçimlendiren 17 Denklem
Kaynak: Clara Moskowitz; The 11 Most Beautiful Mathematical Equations. Yayınlanma Tarihi: 1 Temmuz 2017; Yayınlandığı Yer: Livescience; Bağlantı: https://www.livescience.com/
Matematiksel










e*iπ
+1=0