Gelişen teknoloji sayesinde erişemediğimiz ya da düzenli veri alımının oldukça zor olduğu bölgeler hakkında uydular sayesinde birçok bilgi toplamaktayız. Peki uydular her yere ulaşabiliyor mu? Hiç düşündünüz mü gözlemleyemediğimiz bölgeler hakkında nasıl bilgi sahibi olabiliriz? Mesela kutuplarda deniz buzulu kalınlığı hesaplamalarını nasıl yapıyoruz?

Deniz buzullarındaki gözlemlenen azalma, küresel iklimi ve ekosistemleri önemli ölçüde etkiliyor. Deniz buzullarının albedo değeri oldukça yüksektir. Bir başka deyişle yüzeye ulaşan güneş ışınlarının çoğunu geri yansıtır. Erime nedeniyle azalan buz örtüsü iklim sistemine giren daha fazla güneş enerjisine neden olur. Sonucunda bu da daha fazla ısınmaya ve daha çok erimeye neden olur.
Deniz Buzulu Kalınlığı Hesaplaması Nasıl Yapılıyor?
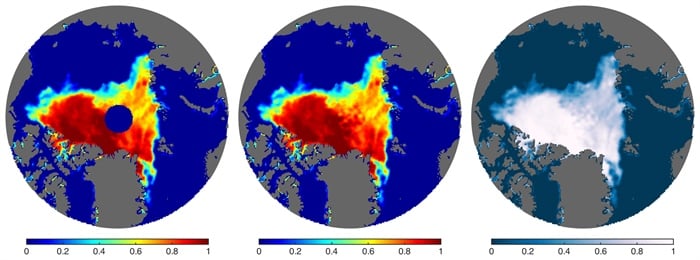
1972 yılından itibaren NASA deniz buzullarını, buz tarafından yayılan mikrodalga ışımalarını ölçen uydular sayesinde gece gündüz izliyor. Bu uydulardan elde edilen veriler 25 km’lik uzamsal çözünürlüğe sahip olup şu ana kadar gözlemleyebildiğimiz en uzun süreli ve en geniş buzul alanına sahip verilerdir. Maalesef, uydunun yörünge eğikliği (orbit inclination) ve uydu üzerindeki cihazın yeryüzünde taradığı alan genişliği (swath) kuzey kutbunu tamamen tarayabilecek durumda olmayıp bu bölgede veri eksikliğine neden olur. (Bakınız Sekil 1, en soldaki görüntü).
Elimizde veri olmadığı bu gibi durumlarda matematiksel modelleme tahminlerde bulunmamızı sağlayabilir. Gelin bu konuyu biraz daha detaylandıralım. Bir bölgedeki buzul konsantrasyonunu hesaplamak için, Strong ve Golden (2016) kısmi diferansiyel denklem tabanlı bir matematiksel model önermişlerdir.
Deniz Buzulu Kalınlığı ve Matematiksel Modelleme
Yeryüzünde Ω bölgesi içerisindeki bir noktayı θ boylamı ve ϕ enlemi ile tanımlayalım. Ω bölgesini veri eksikliğinin olduğu bölge olarak düşünebiliriz. Örneğin Sekil 1’de en soldaki resimdeki kutuplarda görünen dairesel bölge. (θ,ϕ) noktasındaki buzul konsantrasyonunu skaler değerli f(θ,ϕ) fonksiyonu ile ifade edelim. Bu fonksiyonu ilk etapta küresel koordinatlarda tanımlı Laplace denkleminin Δψ = 0 (1) çözümü olarak düşünebiliriz: f(θ,ϕ) = ψ(θ,ϕ)
Laplace denkleminin sınır koşulları veri eksikliğinin bulunduğu bölgenin sınırından, ∂Ω, alınmış gözlemlerle ifade edilsin. (Ψ fonksiyonunun tek çözümü olması için ∂Ω sınırının yeteri kadar pürüzsüz ve buzul konsantrasyonunun ∂Ω sınırı boyunca sürekli bir fonksiyon olması gerekir.) Laplasyeni ikinci dereceden sonlu fark operatörü olarak ifade edersek denklem (1)’in çözümünü sayısal olarak elde ederiz.
Elde edilen çözüm bizim kullandığımız matematiksel modele dayalı olup gerçeğin bir tahminidir. Bu yüzden her zaman gerçeği tam olarak yansıtan rakamlar elde edemeyebiliriz. Peki bu çözümü iyileştirmek mümkün mü? Diğer bir deyişle gerçek çözüme biraz daha yakınlaştırmak? Evet, bunun için hatayı temsil edecek skaler değerli stokastik W(θ,ϕ) terimini matematiksel modelimize dahil edebiliriz: f(θ,ϕ) =ψ(θ,ϕ) + W(θ,ϕ)
W(θ,ϕ) fonksiyonu, ψ(θ,ϕ) fonksiyonunun gerçek değerlerden sapmalarını belirler. Bu fonksiyonun parametlerini veri elde edebildiğimiz bölgelerden toplanan gözlemleri kullanarak bulabiliriz.
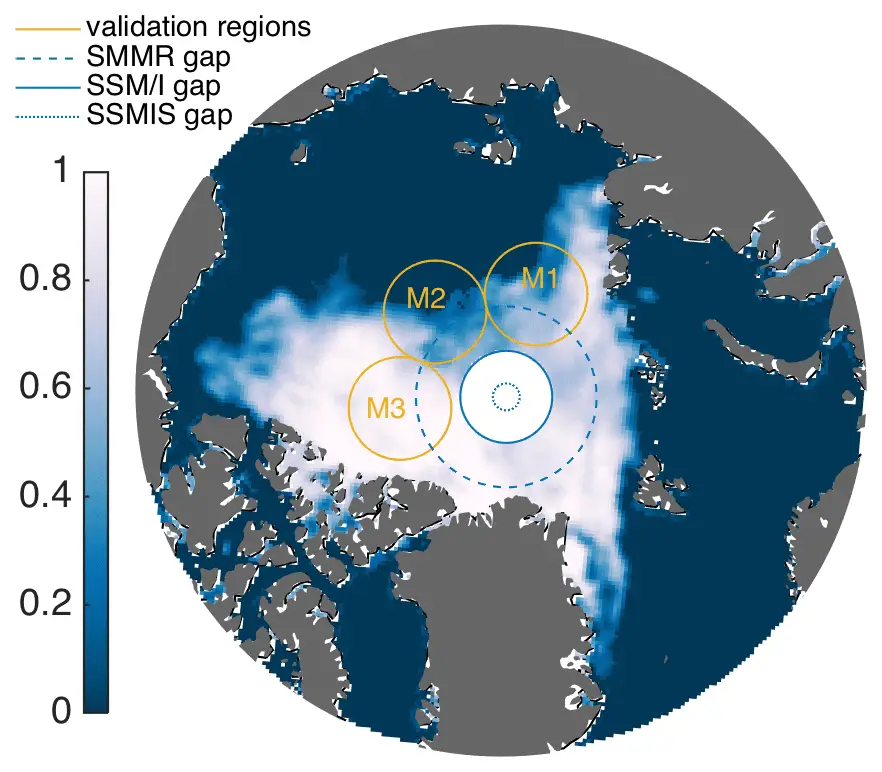
Mesela Sekil 2’de sarı ile gösterilen üç farklı dairesel bölgeden alınan gözlemlerimiz olsun. Gözlemlerin olduğu yerlerde hata terimi. W(θ,ϕ) = f’ (θ,ϕ) – ψ(θ,ϕ) olarak ifade edilir. Burada f’ gözlem konsantrasyonlarının değerlerini verir. Elde edilen binlerce gözlemin analizine dayanarak, W için mevsimsel olarak değişen bir genlik formüle edilmektedir. Bunun sonucunda gerçekçi mekansal otokorelasyon oluşturulur.
Başka bir ifadeyle, bu gözlemler kullanılarak mekansal objelerin arasındaki ilişki uzaklığa ve zamana bağlı olarak belirlenir. Sonrasında bu mekansal otokorelasyon kutup bölgelerinde veri boşluğunun olduğu yerlerde kullanılır.
Sonuç olarak
Laplace denkleminden elde ettiğimiz çözümün hatasını ulaştığımız gözlemlerdeki bilgilere dayanarak en aza indirgeyebiliriz. Sekil 1’de bu yöntemle tahmin edilen buzul konsantrasyonlarını görebilirsiniz. Matematiksel modellemeyi, gözlem verileriyle birleştirilip tahminlerde bulunmak güncel uygulamalı matematik problemlerinde çok sık rastlanır. Bu konu ile ilgili olarak ayrıca Veri Bilimi Nedir Ve Uygulamaları Nelerdir? başlıklı yazımıza da göz atabilirsiniz.
Kaynaklar ve ileri okumalar :
- Strong, C., & Golden, K.M. (2017). Filling the Sea Ice Data Gap with Harmonic Functions, SIAM News.
- Strong, Courtenay & Golden, Kenneth. (2016). Filling the Polar Data Gap in Sea Ice Concentration Fields Using Partial Differential Equations. Remote Sensing. 8. 442. 10.3390/rs8060442.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel