Sudoku ve bulmacalar ile ilgili iseniz muhtemelen bugüne kadar Euler’in adı ile anılan 36 Subay bulmacasını duymuş olmalısınız. Uzun zaman aslında tam olarak 243 yıl boyunca çözümünün mümkün olmadığı düşünülen bu problem, biraz ilginç bir biçimde çözülmüş olabilir. 1779’da İsviçreli matematikçi Leonhard Euler, aşağıdaki bulmacayı ortaya atmıştı. Bu problem, bir Pazar gazetesinde bulabileceğiniz bir bilmeceye benziyor.
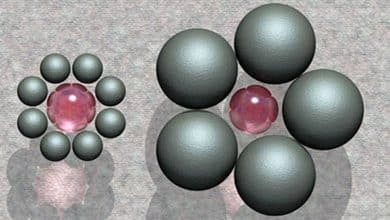
Bir savaş olduğunu hayal edin. Altı alaydan oluşan bir ordunun komutanısınız. Bu alayların her birinde, her biri altı farklı rütbeye sahip altı subay var. Yani komutanızda 36 tane subay var. Bu subayları 6×6’lık bir ızgaraya yerleştirmeniz gerekiyor. Bu matrisin her satırında ve sütununda her alaydan ve her rütbeden sadece bir subay olacak biçimde yerleştirmek mümkün müdür?
Bulmaca, beş rütbe ve beş alay veya yedi rütbe ve yedi alay için kolayca çözülebilmektedir. Ancak 36 subay için bir çözüm aradıktan sonra Euler, “böyle bir düzenlemenin imkansız olduğu, ancak bunu kesin bir şekilde gösteremeyeceği” sonucuna varmıştır.
Bir yüzyıldan fazla bir süre sonra, Fransız matematikçi Gaston Tarry, gerçekten de, Euler’in 36 subayını 6’ya 6’lık bir kareye yerleştirmenin bir yolu olmadığını kanıtladı. 1960’da matematikçiler bilgisayarlardan destek alarak, 6 hariç ikiden büyük herhangi bir sayıda alay ve sıra için çözümün mümkün olduğunu kanıtladı.

Aslında benzer bulmacalar 2000 yıldan fazla bir süredir insanları büyüledi. Yukarıdaki problemi daha iyi anlayabilmek için öncelikle sihirli kareleri anımsamanız gerekiyor. Sihirli kare, içinde 1’den n’e kadar sayıların yazılı olduğu nxn boyutlarında bir karedir. Detaylar için: Sihirli Kareler Basit Bir Kareden Çok Daha Fazlasıdır!
Ancak bu sayılar öyle yazılmışlardır ki her satır, sütun ve köşegenin toplamı aynı sayıya eşittir. Aslında bu soruda karşımıza çıkan sihirli karenin bir özel türü olan Sudoku’nun gerçek ataları olan Latin kareleridir.
Latin Kareleri Hatırlayalım
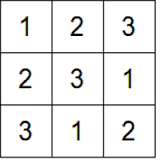
Latin kareleri, sayı, harf veya sembollerle dolu ızgaralardır. Ancak aynı satır veya sütunda bir sembol iki kez görünmez. Örneğin elinizde 1,2 ve 3 rakamları olsun. Sizin bunları rakamların her biri her satır ve her sütunda birer kez bulunacak biçimde 3×3 lük bir ızgaraya yerleştirmeniz gereksin. Aşağıdaki şekil dizebileceğiniz olasılıklardan bir tanesi. Aslında tam 12 tane farklı kare yapabilirsiniz. İşte bu oluşturduğunuz sayı dizinine 3. dereceden Latin Kare denir.
Bu örneği genişleterek istediğiniz dereceden Latin kare oluşturabilirsiniz. Bir Latin kare oluştururken illa sayı kullanmanız gerekmez. Bazen harfler, bazen şekiller kullanarak bu kareleri oluşturabilirsiniz. Sadece 1 ve 2 sayılarını seçerseniz toplam 2 Latin kare elde edersiniz.
1,2,3 sayılarını seçerseniz ilk örnekte de bahsettiğimiz gibi toplam 12; 1,2,3,4 sayılarını seçerseniz 576; 1,2,3,4,5 sayılarını seçerseniz 161 280 farklı dizilim elde edebilirsiniz. Tahmin edeceğiniz gibi bu sayı çok hızla büyüyerek artar. 11 tane sayı seçerseniz karşınıza 776966836171770144107444346734230682311065600000 gibi bir sayı çıkacaktır.
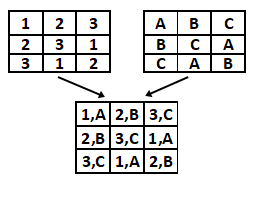
Bazen Latin kareleri birleştirmek gerekir. Bu tür karelere Greko-Latin kareler denir. Aynı zamanda Euler kareleri olarak bilinirler. Greko-Latin karesi, dik Latin karelerinin birleşimi olarak da tanımlanır. Bu kadar bilgiden sonra şimdi sorumuza dönelim. 36 subay problemi bir 6×6’lık bir Greko-Latin karedir.
36 Subay Problemi Nasıl Çözülebilir?
Ve nihayetinde bu problem için bir çözüm bulduk gibi gözüküyor. Ancak bu çözüm bildiklerimizden biraz farklı. Çünkü işin içine kuantum dolanıklığı sokmanız gerekiyor. Çözüm, kuantum nesnelerin ölçülene kadar birden fazla olası durumda olabileceği gerçeğinden yararlanıyor.
Euler’in klasik probleminde, her subayın belli bir alayı ve rütbesi vardır. Ancak kuantum dünyasında bir subay, aynı anda birden fazla alayı veya rütbeyi işgal edebilir. Polonya’daki Jagiellonian Üniversitesi’nden araştırmacı Adam Burchardt, ızgarayı kuantum subaylarla doldurmanın çözümü mümkün kıldığını kanıtladı. Kanıt teknik bilgi gerektirdiği için detaya fazla girmeyeceğiz. Ancak merak edenler buradan inceleyebilirler.
Şimdi bu bizim ne işimize yaradı demiş olabilirsiniz. Araştırmacılar elbette bu kanıtı eğlence olsun ya da bulmaca çözülsün diye yapmadılar. Bu sonuç kuantum iletişimi ve kuantum hesaplama için önem ifade ediyor.
Dolaşık durumlar, bir hata durumunda bile verilerin güvenli olmasını sağlamak için kuantum hesaplamada kullanılmaktadır. Bu sürece de kuantum hata düzeltme adı veriliyor. 36 Subay probleminin kuantum versiyonu ise maksimum bir dolaşıklık durumunu garanti ediyor.
Kaynaklar ve ileri okumalar için:
- The 36 officers problem; https://plus.maths.org/content/36-officers-problem
- Euler’s 243-Year-Old ‘Impossible’ Puzzle Gets a Quantum Solution; yayınlanma tarihi: 10 Ocak 2022; Bağlantı: https://www.quantamagazine.org/
- Centuries-old ‘impossible’ math problem cracked using the strange physics of Schrödinger’s cat; Yayınlanma zamanı: 20 Ocak 2022; Bağlantı: https://www.livescience.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel