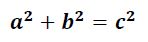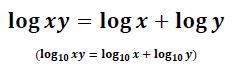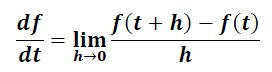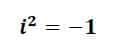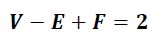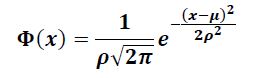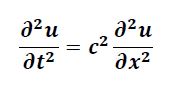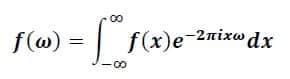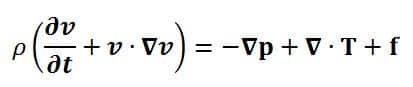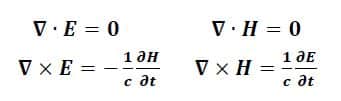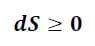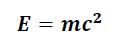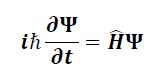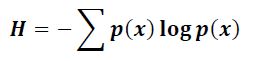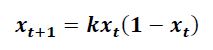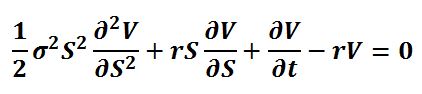Matematik her yerde ve bu 17 denklem dünya anlayışımızı sayısız yollarla şekillendiriyor. Matematik ve insanlık tarihini şekillendiren bu harika 17 denklem hakkında biraz daha bilgi edinelim.
Günümüzü Biçimlendiren 17 Denklem
Pisagor Teoremi
Düz bir düzlem üzerinde bir dik üçgenin kenarları arasındaki ilişkiyi tanımlar. Kısa kenarların uzunluklarının kareleri toplamı (a ve b), uzun kenarın uzunluğunun karesine eşittir, (c). Bu ilişki, aslında Öklid geometrisindeki düz dikme eğriyi, Öklid geometrisi olmayan eğrilerden ayırır. Örneğin, bir kürenin yüzeyinde çizilen üçgen Pisagor teoremine uymak zorunda değildir.
Logaritma
Logaritmalar üstel fonksiyonların tersidir. Belli bir taban için bir sayının logaritması, bize tabanın hangi kuvvet ile çarpıldığını söyler. Şekildeki denklem, logaritmaların en kullanışlı özelliklerinden birini gösterir. Çarpımı toplama çevirir. Bu da çok büyük sayıların çarpımını kolaylaştırır. Logaritmanın keşfi tek kelimeyle devrimdi. Dijital bilgisayar gelişene kadar, bu denklem, büyük sayıları hızlı çarpmanın en yaygın yoluydu. Bu formül fizikte, astronomide ve mühendislikte hesaplamalarını büyük ölçüde hızlandırdı.
Diferansiyel ve İntegral Hesabı
Burada verilen formül, türevin tanım formülüdür. Türev, herhangi bir zaman aralığındaki değişim miktardır. Yani türev değişimi ölçmek için kullanılır. Örneğin hızı konumun türevi olarak düşünebiliriz. Eğer saatte 3 mil (4.8 km) yürüyorsanız, her saatte konumunuz 3 mil değişmiştir. Bilimlerinin çoğu değişimlerle ilgilenmektedir. Türev ve integral hesaplamaları da bu nedenle matematikçilerin ve bilim insanlarının değişim anlayışının kalbinde oturmaktadır.
Yer Çekimi Kanunu
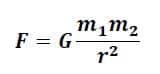
Newton’un yer çekimi yasası formülünde, iki nesne arasındaki çekim gücü F, evrensel sabit G, iki nesnenin kütlesi m1 ve m2ve nesneler arasındaki uzaklık r’dir. Newton’un yasası bilim tarihinin olağanüstü bir parçasıdır. Gezegenlerin niçin o hareketleri yaptıklarını, neredeyse kusursuz bir şekilde açıklar. Ayrıca evrensel doğası da dikkate değerdir. Newton’un yer çekimi kanunu 200 yıl çok iyi ilgi gördü. Ama elbette Einstein’ın genel görelilik teorisinden sonra işler karıştı. (Yazının ilerisinde ona da bakacağız.)
-1’ in Karekökü
Hayali (kompleks) sayılarda bir sayının karesi negatiftir. Buradaki denklemde i bir sayıdır ve bu i sayısı -1’in kareköküdür. İkinci dereceden bir denklem çözümünde deltanın sıfırdan küçük olması durumunda reel kökü yoktur. Ama denklemin kökü yoktur diyemeyiz. Denklem karmaşık köke veya köklere sahiptir diyebiliriz. Matematiksel olarak karmaşık sayılar son derece muazzamdır ve mükemmel bir şekilde çalışır. Hesaplamalar, karmaşık sayılara genişletilebilir. Bunu yaparak, bu sayıların inanılmaz simetrilerini ve özelliklerini bulabiliriz. Bu özellikler karmaşık sayıları elektronik ve sinyal işlemede gerekli kılmaktadır.
Çok Yüzlüler için Euler Formülü
Euler formülünde; “V” bir çok yüzlü geometrik şeklin köşe sayısını , “E” aynı şeklin kenar sayısını, “F” ise aynı şeklin yüz sayısını, ifade eder. Denkleme göre, yüz sayısı ile köşe sayısının toplamından kenar sayısını çıkarırsanız, daima 2 sayısını elde edersiniz.
Basit olarak bir küp düşünelim. Küpte, 8 köşe, 12 kenar ve 6 yüz vardır. Köşeleri ve yüzleri toplar, kenarları çıkarırsam, (8+6-12=2) 2 sayısını elde ederim. Hangi düzgün çok yüzlü geometrik şekli incelerseniz inceleyin yine aynı sonucu elde edersiniz. Örneğin sizlerde aynısını beşgen piramit için yapabilirsiniz.
Euler Formülü topoloji açısından temel öneme sahiptir. Euler’in gözlemi şimdi topolojik değişmez olarak adlandırılanların ilk örneklerinden biriydi. Euler’in Konigsburg Köprüleri probleminin çözümü ile birlikte, bu gözlem; modern fizik için gerekli olan matematiğin bir dalının temelini oluşturan topolojinin gelişimine yol açtı.
Normal Dağılım (Gauss Dağılımı)
Çan eğrisi grafiğine sahip normal olasılık dağılım fonksiyonu, istatistiğin her yerinde bulunur. Denklemde; “ρ”” standart sapmayı , “x” fonksiyonumuzun değişkenini, “μ” sayısı ise ortalama değeri ifade eder. Ortalama değere yaklaştıkça o olayın görülme olasılığı artar. Tam tersine ortalama değerden uzaklaştıkça o olayın görülme olasılığı azalır. Normal eğri, çeşitli özellikleri modellemek için fizik, biyoloji ve sosyal bilimlerde kullanılır. Özellikle modern istatistiğin temelindeki denklemdir. Normal eğrinin çok sık ortaya çıkmasının sebeplerinden biri de bağımsız değişkenlerin geniş gruplarının davranışını tanımlamasıdır.
Dalga Denklemi
Bu bir diferansiyel denklemdir veya yukarıdaki gibi türevin özelliği bakımından özelliklerin zamanla nasıl değiştiğini açıklar. Dalga denklemi, titreşen bir gitar teli, bir taş atıldıktan sonra havuzda oluşan dalgalanmalar veya akkor ampulden gelen ışık dalgalarının davranışını tanımlar.
Fourier Dönüşümü
Fourier dönüşümü insan konuşması gibi daha karmaşık dalga yapılarını anlamak için gereklidir. Konuşan bir kişinin kaydı gibi karışık dalga fonksiyonunu göz önüne alalım. Fourier dönüşümü dağınık işlevi birkaç basit dalganın birleşimine dönüştürerek analizin büyük ölçüde basitleştirilmesine olanak tanır. Zamana bağlı fonksiyonları, frekansa bağlı olarak tanımlamaya yarar. Fourier dönüşümü, modern sinyal işleme ve analizinin ve veri sıkıştırmanın kalbindedir.
Navier- Stokes Denklemi
Dalga denklemi gibi, bu da diferansiyel bir denklemdir. Denklemin sol tarafındaki “ρ” harfi, akışkanın yoğunluğunu ifade eder ve parantezin içinde hızın zamana göre türevi alınmış yani ivmeyi ifade eder. Buradaki ivme bir akışkanın ivmesidir. Parantez içerisindeki ikinci terim, akışın hızı ile akışın gradyanını (değişim vektörünü) birbiriyle çarpan ifadedir.
Denklemin sağ tarafında ise üzerine etki eden kuvvetleri belirtir. (ters üçgen, del operatörüdür. İlk terimde akışın basıncının del operatörü ile çarpımı alınır. Sonrasında ise aynı işlem, toplam stres tensörü ile yapılır ve sonunda bu iki terimin toplamına “f” ile ifade edilen vücut kuvvetleri eklenir.)
Dolayısıyla bu denklem, Newton’un İkinci Yasası’nın F=m.a akışkanlara genişletilmiş bir versiyonudur. Navier-Stokes denklemleri akan akışkanların davranışını tanımlar. Yani, bir borudan geçen su, bir uçak kanadındaki hava akışı veya bir sigaradan çıkan duman bu denklem yardımı ile tanımlanır.
Navier-Stokes denklemlerinin bilgisayarların akışkan hareketi oldukça iyi simüle etmesine olanak tanıyan yaklaşık çözümlerine sahipken, denklemlere matematiksel olarak kesin çözümler üretmek mümkün olup olmadığı halen açık bir soru (bir milyon dolarlık ödül ile) halindedir.
Maxwell’in Denklemleri
Bu dört diferansiyel denklem, elektrik E ve manyetizma H arasındaki davranışı ve ilişkiyi tanımlamaktadır. Elektrik ve manyetik alanları birleştirmeye çalışan ilk kişi Michael Faraday’dır. Onun bu çabasını da ilk olarak James Clerk Maxwell tarafından denkleme dönüştürülmüştür. Bu keşif, fiziği temelden değiştirmiştir. Newton’un hareket yasaları ve evrensel çekim yasası klasik mekaniktir olduğu gibi Maxwell’in denklemleri klasik elektromanyetizmadır. Modern fizik elektromanyetizmanın kuantum mekanik bir açıklamasına dayanır. Bu zarif denklemlerin insan ölçeğinde iyi çalışan bir yaklaşım olduğu açıktır.
Termodinamik’in İkinci Yasası
Kapalı bir sistemde, sistemin entropinin S daima sabit veya artmakta olduğunu gösterir. Termodinamikte entropi kabaca bir sistemin bozukluğunun bir ölçüsüdür. Denklemdeki “dS” ifadesi, entropinin zamana bağlı değişimini ifade eder ve bu değişim her zaman pozitif olmak zorundadır. Yani karmaşıklık (düzensizlik) daima artar.
Termodinamiğin ikinci yasası, zamanın bu şekilde önemli olduğu fizikteki birkaç durumdan biridir. Çoğu fiziksel süreç tersine çevrilebilir – denklemleri bozmadan geriye doğru çalıştırabiliriz. Fakat, termodinamiğin ikinci yasası yalnızca bu yönde çalışır. Eğer siz bir fincan sıcak kahveye bir buz küpü koyarsanız, buz küpünün erimesini her zaman görürsünüz. Ancak asla kahvenin donduğunu göremezsiniz.
İzafiyet Teoremi
Tahmin ediyorum ki hepiniz bu eşitliği bir yerlerde gördünüz ve hakkında az çok bilginiz var. Einstein’ın meşhur denklemi. Einstein, genel ve özel görelilik teorileri ile fizik dersini kökten değiştirdi. Bu denklem, maddenin ve enerjinin birbirine eşdeğer olduğunu belirtir. Özel görelilik, evrensel bir hız sınırı olan ışık hızı ve farklı hızlarda hareket eden insanlar için zaman geçişi gibi fikirleri ortaya attı.
Genel görecelik teorisi, yer çekimini, uzay ve zamanın kendilerini eğip katlanması olarak tanımlar ve Newton’un yasalarından beri yer çekimi anlayışımızda ilk büyük değişikliktir. Genel görecelik, evrenin kökenini, yapısını ve akıbetini anlamamız için gereklidir.
Schrödinger Denklemi
Schrödinger denklemi, bir kuantum sistemi hakkında bize her bilgiyi veren araç dalga fonksiyonu adında bir fonksiyondur. Dalga fonksiyonunun uzaya ve zamana bağlı değişimini gösteren denklemi ilk bulan Avusturyalı fizikçi Erwin Schrödinger’dir. Bu yüzden denklem Schrödinger denklemi adıyla anılır. Kuantum mekaniğinde ana denklem budur. Genel görelilik evrenimizi en büyük ölçeklerinde açıkladığından, bu denklem atomların ve atom altı parçacıkların davranışını yönetir.
Modern kuantum mekaniği ve genel görelilik, tarihteki en başarılı iki bilimsel kuramdır. Kuantum mekaniği, en modern teknoloji için de gereklidir. Nükleer enerji, yarı iletken tabanlı bilgisayarlar ve lazerler, kuantum fenomenleri etrafında oluşturulmuştur.
Bilişim Kuramı
Burada verilen denklem Shannon bilgi entropisi içindir. Yukarıda verilen termodinamik entropi ile olduğu gibi, bu bir bozukluk ölçüsüdür. Bu durumda, bir mesaj, bir kitap, internette gönderilen bir JPEG resmi veya sembolik olarak temsil edilebilecek herhangi bir şeyin bilgi içeriğini ölçer. Bir mesajın Shannon entropisi, içeriğinin bir kısmını kaybetmeden mesajın ne kadar sıkıştırılacağına ilişkin daha düşük bir sınırı temsil eder.
Denklemde sol tarafta yer alan ve “H” harfi gibi gözüken ama Yunan harflerinden biri olan “eta”, entropiyi (düzensizliği) simgeler. Denklemin sağında ki “p(x)” incelemekte olan fonksiyonu gösterir. Bu fonksiyon, seri toplama ifadesi altında aynı fonksiyonun logaritmasıyla çarpılmaktadır.
Bu denklem, bilginin matematiksel çalışmasını başlattı ve sonuçları bugün ağlar üzerinden nasıl iletişim kurduğumuzun merkezinde yer almaktadır. Ian Stewart’a göre: “Bilgi çağını başlatan denklem bu olmuştur.”
Kaos Teorisi
Bu denklem May’ın lojistik haritasıdır. Zamanla gelişen bir süreci açıklar xt+1 bir sonraki zaman periyodunda bir miktar x seviyesi). k, seçilen bir sabittir. Belirli k değerleri için harita kaotik davranışı* gösterir: x’in belirli bir başlangıç değerinden başlasak süreç bir şekilde gelişir, ancak herhangi bir başlangıç değerinden başlarsak, hatta ilk değere çok yakın bir başlangıç yaparsak, süreç tamamen farklı bir şekilde gelişecektir.
Bir çok alanda kaotik davranışları görebiliriz. Hava, klasik bir örnektir. Bir gün atmosferik koşullarda ufak bir değişiklik, birkaç gün sonra tamamen farklı hava koşullarına yol açabilir. Bu hava sistemlerinin çoğu, bir kıtada kanatlarını çırpan bir kelebek, başka bir kıtada kasırgaya sebep olabilir.
Daha iyi anlamak adına; mesela kalabalık bir meydandan 200 metre yukarı çıktığınızı hayal edin. Aşağı baktığınızda kalabalığın amaçsızca karışık bir şekilde sağa sola gittiğini görürsünüz. Sonra o kalabalığın içine indiğinizi ve her bir bireyi takip edebileceğinizi hayal edin. O zaman anlayacaksınız ki aslında bir kargaşa yok. Her bir bireyin bir amacı olduğunu ve ona göre hareket ettiğini anlarsınız. İşte buna Kaos Teorisi deniyor. Karışıklığın düzeni dersem daha iyi anlaşılır.
Black- Scholes Denklemi
17 denklemin sonuncusu olan, diferansiyel bir denklem olan Black-Scholes, finans uzmanlarının ve tüccarların türev finansal araçlarla ilgili fiyatları nasıl bulduklarını açıklıyor. Türev modern finansal sistemin önemli bir parçasıdır. Denklemdeki “σ” bir malın fiyatlarındaki dalgalanmayı, “S” malın fiyatını, “V” zamana ve mal fiyatına bağlı bir fonksiyonu, “r” yıllık risksiz faiz miktarını belirtir. Denklemde karmaşık bir türev hesabı yapılarak fiyatlar belirlenmeye çalışılmaktadır.
Black-Scholes denklemi, finansal profesyonellerin türev niteliğine ve esas alınan varlığa dayanarak bu finansal ürünlerin değerini hesaplamalarına olanak tanır. Fischer Black ve Myron Scholes bu keşifleri sayesinde 1977 yılında Nobel Ekonomi Ödülü’nü almışlardır.
Ayrıca bir başka seçkiye de bu yazımızdan erişeceksiniz: Bilim İnsanlarının Seçtiği En Güzel 10 Denklem
Yararlanılan Kaynak: The 17 Equations That Changed The Course of History; http://www.sciencealert.com/t
Matematiksel