
Haberlerde herhangi bir deprem haberi yer aldığı zaman muhtemelen “Dün X şehrini 7,2 büyüklüğünde deprem vurdu” gibi bir ifadeyle karşılaşacaksınız. Bu cümle ne anlama geliyor? Aktırılan bilgileri nasıl yorumlamalısınız? Konu hakkında kısa bir bilgilendirme yapalım.
Deprem büyüklüğü, bir deprem tarafından salınan enerji miktarını temsil eden bir sayıdır. Bir sismometre tarafından kaydedilen yer sarsıntısının genliğinin ölçülmesiyle belirlenecektir. Depremin gücü aslında iki yolla ölçülmektedir. Bunlardan birisi depremin “şiddetini” diğeri ise “büyüklüğünü” ölçmeye yöneliktir. Bu nedenle duyduğumuz sayılar bazen Richter ölçeği bazen de Mercalli Ölçeği biçimindendir. Bu iki derecelendirme, bir depremi iki farklı açıdan tanımlar.
Depremler, yerkabuğu içindeki kırılmalar nedeniyle ani olarak ortaya çıkan titreşimlerin dalgalar halinde yayılmasıyla oluşur. Depremler ile ilgili çalışan bilim dalı ise sismolojidir. Sismoloji ile ilgili bazı tanımlamaları anlamak hem yazının devamını kavramanız hem de duyduğunuz haberlerin arka planı hakkında daha fazla bilgi edinmeniz açısından faydalı olacaktır.
“Jeolojiyi depremden sonraki sabah öğreniyoruz.”
Ralph Waldo Emerson.
Deprem Dalgalarını Anlamak: P ve S Dalgası Nedir?
Bir deprem esnasında odak noktasından hızla sismik dalgalar yayılacaktır. Bu sismik dalgalar iki türde karşımıza çıkar. Bunlar yerin iç kısımlarındaki odak noktasından başlayıp her yöne doğru yayılan “cisim dalgaları” ve merkez üssünden yayılan ve yer yüzeyinde ilerleyen “yüzey dalgaları”dır.
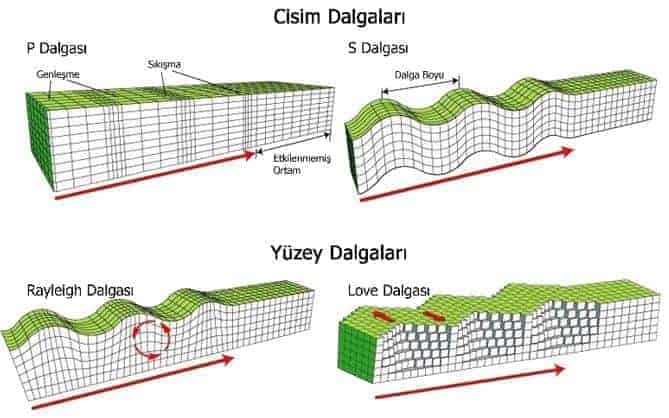
Yer kabuğunun iç kısımlarında etkili olan cisim dalgalarının da P-dalgaları ve S-dalgaları olmak üzere iki türü var. P-dalgaları, “birincil” anlamındaki İngilizce “primary” sözcüğünden gelir. Bu dalgalar en hızlı ilerleyen ve deprem ölçüm istasyonlarına ilk ulaşan sismik dalgalardır. Birinci sözcüğü bu nedenle kullanılmaktadır. P-dalgalarının diğer önemli özelliği, katı kaya kütleleri içinde, sıvılarda ve havada ilerleyebiliyor olmasıdır.
İkinci tür cisim dalgaları olan S-dalgaları da, İngilizce “ikincil” anlamına gelen “secondary” sözcüğünden gelir. Bu dalgalar daha yavaş hareket ettiği için bu ismi almıştır. S-dalgaları yalnızca katı kaya kütlelerinde ilerleyebilirler ve ilerlerken de kayaları aşağı-yukarı, sağa-sola doğru hareket ettirirler.
Sismik dalgaları belirlemekte kullanılan aygıtın adı sismometre denir. Sismometre tek başına, ölçtüğü hareketi kaydedemez. Bu iş için sismograflar kullanılmalıdır. Dünya üzerinde, depremleri kaydeden ve birbirleriyle iletişim halinde olan binlerce sismograftan oluşmuş bir ağ vardır. Bu sayede de depremin ardından geçen birkaç dakika içinde, sismograflar sismik dalgaları algılamaya başlarlar. Deprem büyükse, Dünya üzerindeki tüm sismograflar tarafından algılanacaktır.
Richter Ölçeği Nedir?
Bir deprem için en yaygın ölçüm standardı, 1935’te California Teknoloji Enstitüsü’nden Charles F. Richter tarafından geliştirilen Richter ölçeğidir. Richter ölçeği, bir depremin büyüklüğünü, yani saldığı enerji miktarını derecelendirmek için kullanılır. Bu, bir sismograf tarafından toplanan bilgiler kullanılarak hesaplanır.
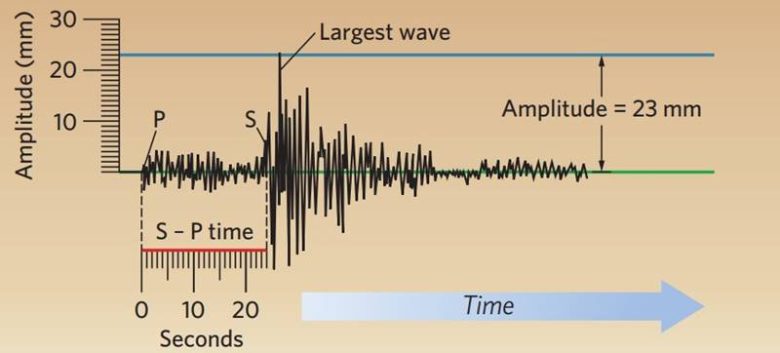
merkez üssüne olan mesafeyi belirlemek için S dalgalarının ve P dalgalarının varış zamanları arasındaki fark hesaplanacaktır.
Richter, merkez üssünden 100 km uzaklıkta ve sert zemine yerleştirilmiş özel bir sismografla kaydedilmiş zemin hareketinin mikron cinsinden ölçülen maksimum genliğinin 10 tabanına göre logaritmasını bir depremin “büyüklüğü” olarak tanımlanır. “Richter Ölçeği” bu standartı temel alır. Sonucunda da 0’dan 8,9’a kadar olan rakamlar kullanır. Rakamlar büyüdükçe depremin büyüklüğü de “logaritmik” olarak artar.
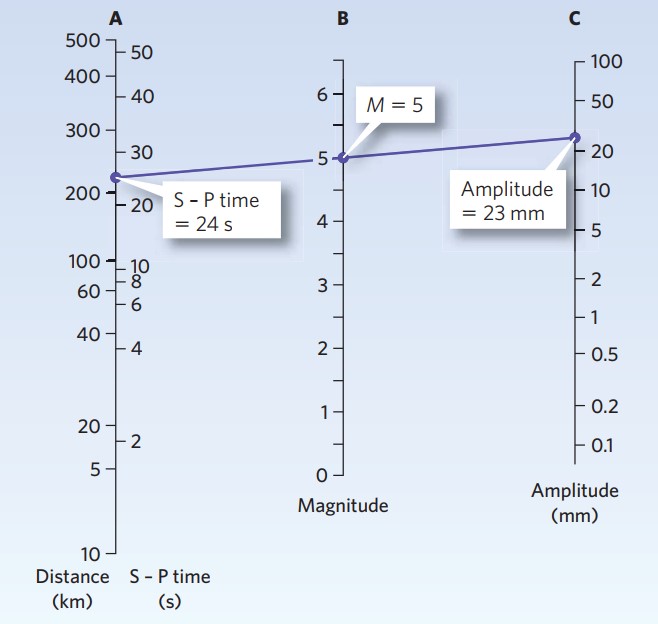
Bunun anlamı şudur. Her ne kadar depremler için 6, 7, 8 gibi birer artan ifadeler kullanılsa da aslında formül 10 tabanlı bir logaritma içerdiği için bu sayılar logaritmik olarak 10’ar artarlar. Yani 6 olarak derecelendirilen bir deprem 3 olarak derecelendirilen bir depremden 6-3=3 ise 10.10.10= 1000 kat güçlü bir etkiye sahip olacaktır.
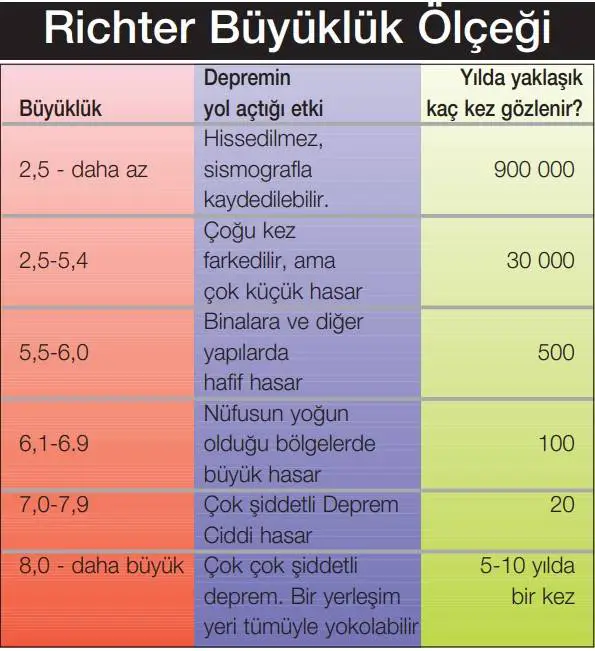
Bugünlerde sismologlar, bir depremin büyüklüğünü temsil etmek için daha doğru bir ölçek olarak kabul edilen moment büyüklük ölçeği adı verilen bir ölçek kullanıyorlar. Bir depremin moment büyüklüğünü (kısaltılmış Mw) hesaplamak için sismologlar birkaç farklı sismik dalganın genliklerini, fay üzerindeki kayma alanının boyutlarını ve meydana gelen yer değiştirmeyi hesaba katarlar. Moment büyüklüğü ölçeği, Richter ölçeği gibi logaritmiktir. Deprem tartışmalarını kolaylaştırmak için sismologlar bir depremin büyüklüğünü tanımlamak için tanıdık basitleştirilmiş tablolar kullanacaklardır. Aşağıdaki tablo buna bir örnektir.
Depremlerle Enerji Salınımı Nasıl Hesaplanır?
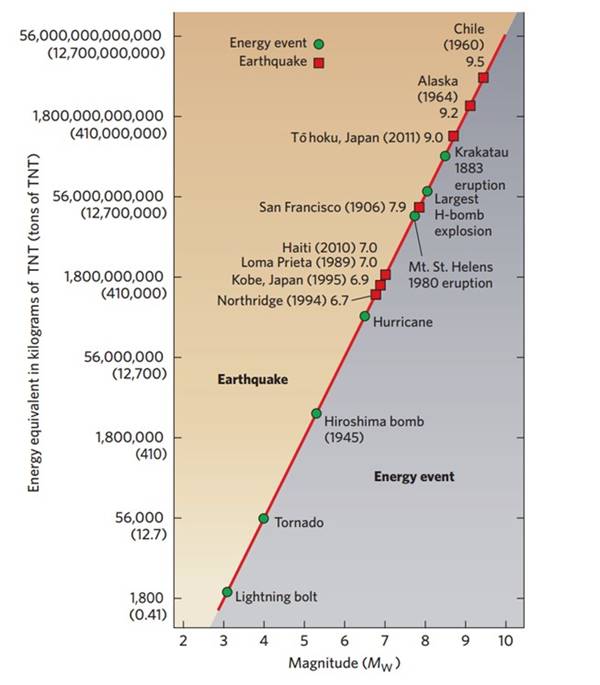
Bir deprem tarafından salınan enerji miktarı hakkında bir fikir vermek için sismologlar, depremleri diğer enerji salan olaylarla karşılaştırırlar. Bazı tahminlere göre, Mw 5.3 büyüklüğündeki bir deprem Hiroşima’ya atılan atom bombası kadar ve Mw 9.0 büyüklüğündeki bir deprem şimdiye kadar patlatılan en büyük hidrojen bombasından önemli ölçüde daha fazla enerji açığa çıkaracaktır.
Büyüklükteki bir birimlik bir artış, yer hareketinin maksimum genliğinde on katlık bir artışı temsil etse de, enerji salınımında 32 katlık bir artışı temsil eder. Bu nedenle, bir Mw 8 depremi, bir Mw 4 depreminden yaklaşık 1 milyon kat daha fazla enerji açığa çıkarır. Depremler tarafından salınan enerji, büyüklükle birlikte önemli ölçüde artar. Büyük depremler, aşağıdaki çizelgede de gördüğünüz gibi en büyük nükleer bombalardan çok daha fazla enerji açığa çıkarır.
Depremin Şiddeti İle Büyüklüğü Aynı Şey Değildir
Depremin gücü aslında iki yolla ölçülmektedir. Bunlardan birisi depremin “şiddetini” diğeri ise “büyüklüğünü” ölçmeye yöneliktir. Şiddet ve büyüklük kavramları sık sık karıştırılsa da aslında farklı şeylerdir. Depremin ne tür ve ne kadar zarar verdiğini ölçmeyi amaçlayan, yani depremin insanlar, binalar ve doğa üzerindeki etkilerini saptayan yöntem aslında “şiddet” ölçümüdür.
Richter derecelendirmeleri, size bir depremin gerçek etkisi hakkında yalnızca kabaca bir fikir verir. Sonucunda bir depremin yıkıcı gücü, bir alandaki zeminin bileşimine ve insan yapımı yapıların tasarımına ve yerleşimine bağlı olarak değişir. Bu nedenle hasarın boyutu Mercalli ölçeğine göre derecelendirilir.
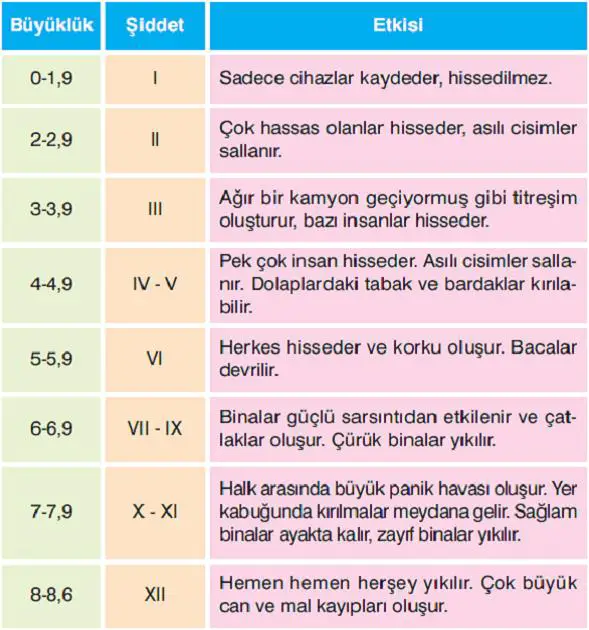
Bir depremin Richter ölçeği derecelendirmesini depremden hemen sonra belirlemek mümkündür. Öte yandan Mercalli derecelendirmesi depremin ardından yapılmaktadır. Uygun bir derecelendirmeye karar vermek için de Mercalli kriterlerini kullanılmaktadır.
Depremin Ne Zaman Olacağını Tahmin Etmek Mümkün mü?
Sismologların depremleri tahmin etmesi mümkün mü? Cevap, tahminin zaman çerçevesine bağlıdır. Sismik kuşakların dağılımına ve depremlerin meydana gelme sıklığına ilişkin mevcut anlayışımızla, uzun vadeli tahminler yapmaları mümkündür. Bu nedenle bir depremin İstanbul’u sarsacağını kesin olarak söyleyebilirler.
Depremler İçin Uzun Vadeli Tahminler Nasıl Yapılmaktadır?
Uzun vadeli bir tahmin, belirli bir zaman diliminde bir depremin meydana gelme olasılığını tahmin eder. Örneğin bir sismolog, “Bu şehirde önümüzdeki 50 yılda büyük bir deprem olma olasılığı %20” demiş olsun. Bu cümle, 50 yıl geçmeden önce bir deprem olma ihtimalinin 5’te 1 olduğunu ima edecektir. Sismologlar, uzun vadeli tahminlere yol açan çalışmaları sismik risk değerlendirmesi olarak adlandırırlar.
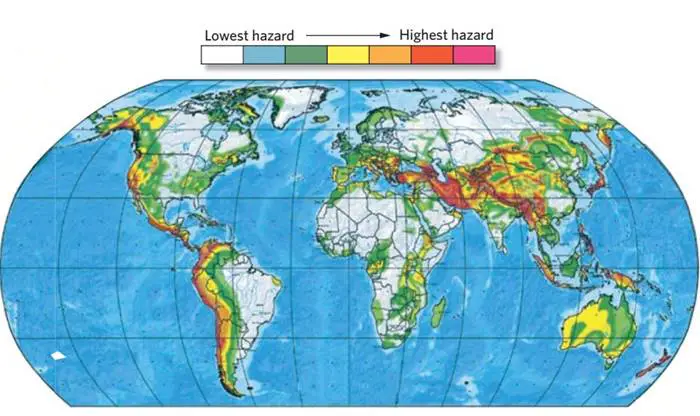
Sismik risk değerlendirmesinin temel dayanağı şu şekildedir. Geçmişte çok sayıda depremin meydana geldiği bir bölgede gelecekte de deprem olma olasılığı yüksektir. Sismik kuşaklar—birçok depremin meydana geldiği bölgeler—bu nedenle, yüksek sismik risk taşıyan bölgelerdir. Bu, depremlerin sismik bir kuşaktan uzakta gerçekleşemeyeceği anlamına gelmez. Ancak herhangi bir zaman aralığında bu tür yerlerde bir deprem olma olasılığı daha düşüktür.
Bununla birlikte, sismologlar doğru kısa vadeli tahminler yapamazlar. Örneğin bundan 40 gün sonra bir İstanbul depremi olacağını söyleyemezler. Daha spesifik bir deprem olasılığı duygusu sağlamak için sismologlar, bir bölgede belirli bir büyüklükteki depremler için tekrar aralığını, belirlemeye çalışırlar. Örneğin, bir bölgede Mw 7 büyüklüğünde bir depremin tekrarlanma aralığı 100 yıl ise, böyle bir depremin yıllık olasılığı 1/100 veya %1’dir.
Belirli bir sismik kuşaktaki büyük depremlerin tekrarlanma aralığını belirlemek için sismologlar, o kuşakta önceki depremlerin ne zaman olduğunu belirlemelidir. Tarihsel kayıtların çok sayıda büyük olayı ortaya çıkaracak kadar geriye uzanmadığı yerler için, araştırmacılar jeolojik kayıtlarda korunan büyük depremlerin kanıtlarını ararlar. Tekrarlama aralıklarına ilişkin bilgi, sismologların sismik tehlikeyi gösteren bölgesel haritaları iyileştirmesine olanak tanır.
Depremler İçin Kısa Vadeli Tahminler Yapılamaz
Bir depremin belirli bir tarihte veya günlerden yıllara kadar bir zaman aralığında gerçekleşeceğini belirten kısa vadeli tahminler düzmecedir. Aslında, bu tür tahminler muhtemelen hiçbir zaman güvenilir olmayacaktır.
Ancak tahmin, gerçek bir sinyale dayanan ve potansiyel olarak hayat kurtarabilen bir deprem erken uyarı sistemi kavramıyla karıştırılmamalıdır. Bir erken uyarı sistemi şu şekilde çalışır: Bir deprem olduğunda, ürettiği sismik dalgalar Dünya’nın içinde dolaşmaya başlar. Merkez üssü ile bir şehir arasına yerleştirilen sismometreler, sismik dalgaları şehre ulaşmadan önce tespit edeceklerdir.
Bu sismometreler depremi algıladığı anda, bir verici, şehre otomatik olarak acil durum sinyalleri gönderir. Neredeyse ışık hızında hareket eden bu sinyaller, sismik dalgalardan birkaç saniye ila bir dakika önce şehre ulaşır. Sinyallerin gelmesi, gaz boru hatlarının, trenlerin, nükleer reaktörlerin ve elektrik hatlarının otomatik olarak kapanmasını sağlar. Ayrıca sinyaller sayesinde insanlar önlem almaları konusunda uyarılır.
Toplumlar makul önlemler alarak depremlerin sonuçlarını hafifletebilir veya azaltabilir. Ne yazık ki doğanın güçlerine karşı şu an elimizde tam kesinleşen bir bulgu yok. Bu nedenle bu konu hakkında farkındalık düzeyimizi arttırmamız oldukça önemli bir konudur. Göz atmak isterseniz: Tarihteki En Büyük Deprem Bir Uygarlığı Neredeyse Yok Etti!
Kaynaklar ve ileri okumalar:
- How Earthquakes Work; Bağlantı: https://science.howstuffworks.com/
- Richter scale; https://www.britannica.com/
- Earth science : the Earth, the atmosphere, and space / Stephen Marshak, University of Illinois at Urbana-Champaign, Robert Rauber, University of Illinois at Urbana-Champaign.
Matematiksel










