
Cebir, algoritma, alkali gibi terimleri düşünün. Bilimin kalbinde yer alan bu kelimeler Arapça kökenlidir. Hristiyanlığın karanlık çağlarını yaşadığı dönemlerde Avrupa’da yaşayan bilim insanları yazıtlarında sıklıkla İslam bilginlerine atıfta bulunur. Bu İslam bilgilerinden en önemli olanlarından ve modern bilime şekil verenlerden biri de tam adı ile Ebu Abdullah Muhammed Bin Musa el Harezmi olarak bilinir. (780-850)
El Harezmi, Abbasi Döneminin tanınmış matematik, coğrafya ve astronomi uzmanıdır. Onun sayesinde Avrupalı bilginler kullanılmakta oldukları Romen rakamları ile aritmetik yapmanın zorluğunu fark etmiştir. Harezmi onlara aritmetik hesaplamalar yapmanın daha kolay bir yolu olduğunu göstermiştir.
Abbasiler döneminde başlayan “Bilimde Müslümanların Altın Çağı” 750-1258 yılları arasına denk gelir. Halife el-Memun, Bağdat’ta Beyt-ül Hikmet adlı bir bilimsel akademi, bir rasathane ve bir kütüphaneden oluşan bir yer açmıştı.

Bilinen adı ile “Bilgelik Evi” doktorların, hukukçuların, müzikçilerin, şairlerin ve bilim insanlarının bir arada toplandığı bir mekan halini almıştı. Burada değerli kitaplar toplanıp Arapça ’ya çevrildi. Bu yer zamanla dönemin en zengin kütüphanesini, gözlem evini ve çoğunlukla matematik, astronomi ve yer bilimleri ağırlıklı, çeşitli çalışma birimlerini içine alan, çevrenin en yetkin bilim adamlarını toplayan, bir araştırma merkezi ve akademisi oldu. Ek okumalar için: Beytül Hikme (Bilgelik Evi): 10. Yüzyılda Bağdat’ta Bilginin Zirve Yaptığı Yer
Harezmi burada çeşitli matematiksel problemlerin çözümü üzerinde çalışıyordu. O esnada, Hintli matematikçilerin yeni çalışmalarını duydu. M.S. 825 tarihlerinde Halife Memun’un izni ile, Hint matematiğini izlemek üzere Hindistan’a gitti.
Burada Aryabhatta’nın (MS 476 – 550) geliştirdiği bir sayı sistemi ile karşılaştı. Bu yeni sayı sistemini ve aritmetiği bütün yönleri ile inceleyip bilgi yükü ile Bağdat’a döndü. Harezmi, “Hindu Hesaplama Sanatı” adlı çalışmasını kaleme aldı.
Aryabhatta ve El Harezmi Elele: On Tabanlı Rakam Sistemi
Devamında matematiğin geleceği için talihli bir olay gerçekleşti. Aryabhatta ve Harezmi en etkili biçimde yüzyıllar üzerinden el ele tutuştular. On tabanlı rakam sistemini geliştirerek ve kullanarak, bu iki matematikçi matematik tarihine devamlılığını koruyan katkıda bulundular.
İşte bu nedenle günümüzde kullandığımız rakamlar Hint – Arap rakam sistemi olarak bilinmektedir. Yazdığı kitap Latinceye çevrildiği zaman, Harezmi’nin ismi Algoritmi oldu. Ve işte bu da günümüze yön veren algoritma sözcüğünün kökenini oluşturdu.

Harezmi. matematik ile uğraşmanın sayılar ile değil sayıları sembolize eden şekillerle olması gerektiğini düşünüyordu. Bu matematikçileri, problemlerdeki karmaşık sayılara saplanıp kalmadan rahatça çözebilmelerini sağladığı için özgürleştirici bir düşünce biçimiydi.
Harezmi kaleme aldığı “El Cebir V’el Mukabele” adlı eserinde (Modelleyerek ya da Dönüştürerek Hesaplama) ilk defa cebir kelimesini kullandı. Bu nedenle Harezmî (Diophantus ile birlikte) “cebirin babası” olarak da bilinir. Matematiği x ve y gibi sembollerle yapabiliyor olmamızı bu keşfe borçluyuz. Harezmi kitabında, semboller kullanmamıştı. Her şeyi sözlü olarak ifade etmişti. Ancak denklemlerin cebir kullanılarak nasıl çözülebileceğini anlatmıştı.
Harezmi’nin Denklem Çözme Mantığı
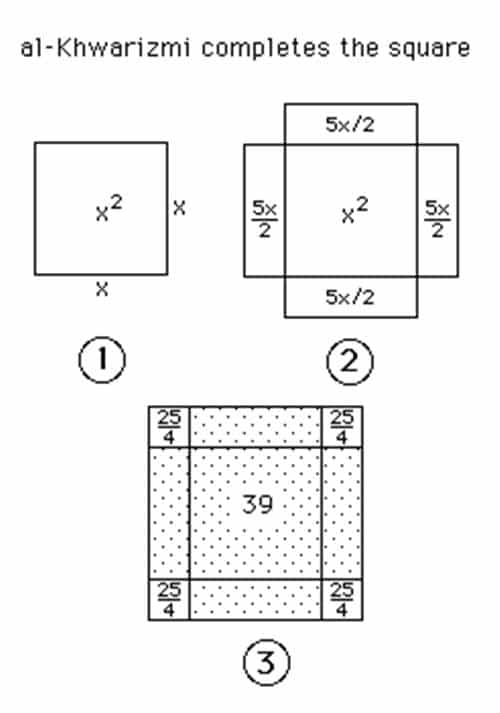
Onun düşünce mantığını kavramak için bir örnek üzerinden gidelim. Denklemimiz x2+10x=39 olsun. Bu denklem Harezmi tarafından bu denklemi “Hangi sayının karesi, sayının 10 katı ile toplanırsa 39 eder?” biçiminde ifade edilmekteydi.
Günümüzde öğrencilere ezberletilen ikinci dereceden denklemin köklerini bulan formül bu anlatım biçiminden türetilmiştir. Burada x2 terimi kenar uzunluğu x olan bir kareyi temsil eder. Denklemdeki +10x terimi ise kenar uzunluğunun 10 katının, karenin alanına eklendiğini gösterir. Denklemin sağındaki 39 sayısı, karenin alanına kenarın 10 katı eklendikten sonraki toplam alanın değeridir. Diğer bir deyişle, x2 +10x teriminin temsil ettiği yeni alan 39’a eşittir.
Harezmi, alanı 39 olan şekli, kareye tamamlamak ister. Böylece yeni (hayali) karenin kenar uzunluğunu hesaplayabilecektir. 10x terimi ile gösterilen dikdörtgenin alanı 4 eşit parçaya bölüp, kenar uzunluğu x olan orijinal karenin dört tarafına ekler. Bu dikdörtgenlerin bir kenarı x uzunlukta olacağı için, diğer kenar doğal olarak 10/4 veya 5/2 olur.
Yeni şeklin toplam alanı 39’a eşittir. Ancak yeni şekil henüz kare değildir, çünkü köşelerde dört küçük boşluk vardır. Köşelerdeki boşluklar, kenar uzunluğu 5/2 olan karelerdir. Bu nedenle her küçük karenin alanı, 5/2’nin karesine eşittir veya 25/4’tür. Dört küçük karenin toplam alanını bulmak için 25/4’ü 4’le çarpınca 25 çıkar.
Bir önceki yeni şeklin alanı 39 idi, bu alana 25 eklenince 64 çıkar. Buradan da karenin bir kenarını 8 bulur. 8 sayısından iki küçük karenin kenar uzunluğunu çıkartarak, x değerini bulur. Küçük karelerin kenar uzunlukları 5/2 idi. İki küçük karenin kenarlarının toplamı, 2 çarpı 5/2 yani 5’tir. Büyük karenin kenar uzunluğu olan 8’den 5 çıkarılınca x değeri 3 olarak bulunacaktır. Sonucunda gördüğünüz gibi ikinci dereceden bir denklemi geometri yardımı ile de çözmek mümkündür. Ayrıca göz atmak isterseniz: Meryem el-Usturlabi: Bilinen İlk Müslüman Kadın Astronom
Kaynaklar ve ileri okumalar:
- Why algorithms are called algorithms. Bağlantı: https://www.bbc.co.uk/ideas/
- Francesn Benson Stonaker – Meşhur Matematikçiler
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









