On dokuzuncu yüzyılın sonuna kadar hiçbir matematikçi sonsuzu, kesinlikle ulaşılamaz bir değer olduğu düşüncesinin ötesinde tanımlamayı başaramamıştı. Georg Cantor böylesine soyut bir kavramı tam olarak ele alan ilk kişiydi ve bunu küme teorisini geliştirerek yaptı.
Fransız matematikçi Henri Poincaré (1854–1912), Cantor’un fikirlerinden matematik disiplinini etkileyen “ciddi bir hastalık” olarak bahsetmiştir. Alman matematikçi Leopold Kronecker (1823-1891) Cantor’a şahsen saldırarak onu “şarlatanlık” ve gençliği yozlaştırmakla suçlamıştır. Peki Georg Cantor ile ilgili bu kadar tartışmalı olan nedir? Bunu anlayabilmeniz için öncelikle onu kısaca tanımanız gerekiyor.
Kısaca Georg Cantor Kimdir?
Georg Cantor (3 Mart 1845-6 Ocak 1918) anne ve babasının Danimarka’dan göç ettiği St. Petersburg’da (Rusya) doğmuş olmasına rağmen hayatının çoğunu Almanya’da geçirdi. Okul yılları boyunca matematikte olağanüstü beceriler sergiledi. 1860’ta liseden üstün başarı ile mezun oldu. Daha sonra İsviçre Federal Politeknik ve Berlin Üniversitesi’nde matematik okudu.

1867’de Georg Cantor, Sayılar teorisine dayalı teziyle Berlin’den doktora derecesi aldı. Daha sonra akademik kariyerinin çoğunu çoğunu geçirerek olduğu Halle Üniversitesi’nde ders vermeye başladı. Sonsuzluk kavramı, genç yaşlardan itibaren ilgisini çekti ve otuzlu yaşlarında, matematiksel sonsuzlukla ilgili çeşitli fikirleri resmileştirdiği küme teorisini geliştiren makaleler yayınladı.
George Cantor’un Fikirleri Zamanın Doğasına Uygun Değildi!
Cantor’a kadar olan matematikçiler için sonsuzluk, matematiğin içine yerleştirilmesi pek de mümkün olmayan bir yerde duruyordu. Bu kavram matematikten daha çok teolojinin ilgi alanına giriyordu. Cantor’a göre kümeler, sonlu veya sonsuz elemanlara sahip olabilen nesnelerin koleksiyonları idi. Örneğin, bir elin parmakları kümesi sonlu elemanlara ({başparmak, işaret parmağı, orta, yüzük ve serçe parmağı}) sahipken, doğal sayılar kümesi (N = {0, 1, 2, 3, 4, 5, 6) …}) sonsuz elemana sahipti.
Günümüzde bu sözleri hemen hemen her öğrenci bilse de Cantor zamanında bu düşünce biçimi devrim niteliğindeydi. Cantor ayrıca kardinal sayılardan bahsetmeye başlamıştı. Kardinal Sayılar: Bir grupta ‘kaç tane‘ nesne olduğunu belirten ve saymada kullandığımız sayılardır. Örneğin bir elin parmakları kümesinin kardinal değeri beş (5) ve doğal sayılar kümesinin kardinal değeri sonsuzdur (∞).
Yıllarca yazıştığı meslektaşı Richard Dedekind 1872’de sonsuz kümeleri zaten düşünmüştü. Ancak Cantor aynı zamanda tüm sonsuz kümelerin aynı boyutta olmadığını da fark etti. Başka bir deyişle, farklı kardinallere sahip sonsuz kümeler de vardı.
Tüm bunları kabullenmeye çalışan insanların henüz logaritma tablolarıyla hesap yapmaya çalışan insanlar olduğu düşünülünce, onu anlamamış olmaları aslında oldukça normaldi. Georg Cantor insanların çığır açan fikirleri er geç kabul edeceğini biliyordu. Ancak ne yazık ki bunun bedeli olarak da ruh sağlığını kaybedecekti.
Bir Sonsuzluk Diğerinden Nasıl Büyük Olur?
Doğal sayılar kümesi (N = {0, 1, 2, 3, 4, 5, 6…}) biçimindedir. B kümenin bir alt kümesi olan asal sayılar kümesi ise (P = {2, 3, 5, 7, 11, 13…} biçiminde olacaktır. Ancak Cantor, her ikisinin de aynı kardinal ve dolayısıyla aynı sonsuz sayıda elemente sahip olduğunu gösterdi. Bunu göstermek için, bir kümeyi oluşturan öğelerin her birini diğerinin öğeleriyle eşleştirdi. Aslında bugün tam olarak ne işe yaradığını bilmeden öğrendiğimiz 1-1 eşleşmeyi uyguladı.
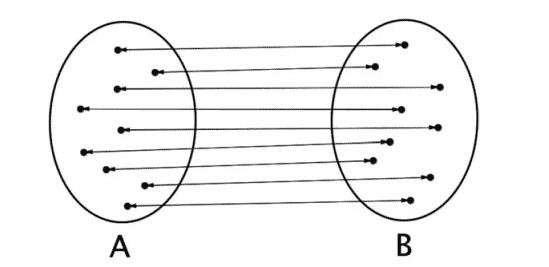
Cantor’un bire bir eşleşme kavramı, iki sonsuz grubu karşılaştırmamızı sağlar. Çünkü kümelerin her birindeki elemanların sayısını gerçekten ayrı ayrı saymak ve sonra sayıları karşılaştırmak zorunda değilizdir. Sadece iki kümenin elemanları arasında bire bir ilişki kurup kuramayacağımızı bulmamız gerekiyor.
Cantor bize tam sayılar ve doğal sayılar kümelerinin eşit büyüklükte olduğunu göstermiştir. Hatta Cantor, rasyonel sayıların da doğal sayılarla bire bir eşleşmeye sokulabileceğini bile göstermiş ve bir biçimde bu kümenin sayılabilir olduğunu kanıtlamıştır.
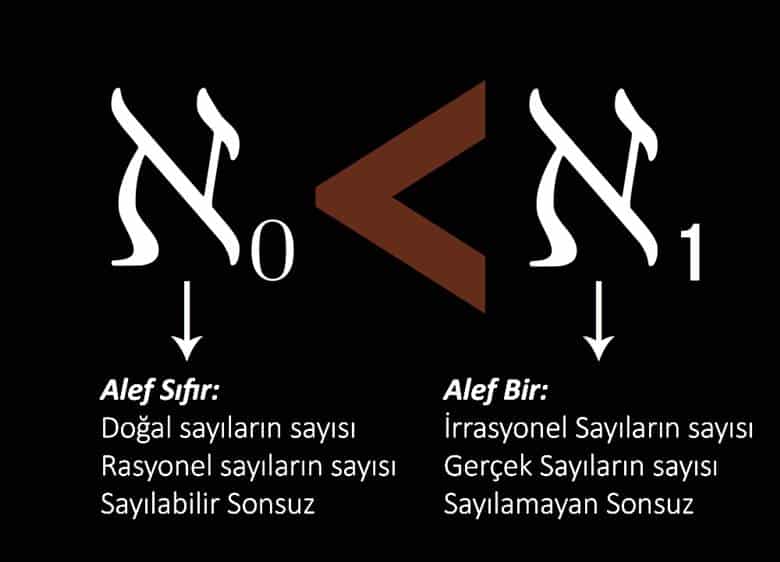
Ancak gerçek sayıların doğal sayılarla bire bir eşlemeye koymanın mümkün olmayacağını da kanıtlamıştır. Böylece gerçek sayılar kümesinin kardinalitesinin doğal sayılar kümesinden daha büyük olduğu sonucuna varmıştı. Bunun anlamı ise bunların farklı boyutlarda sonsuzluklar olmasıydı.
Tüm bu sonsuz kardinallerin en küçüğüne, doğal sayıların kardinal sayısına, alef-sıfır (alef, İbrani alfabesinin ilk harfidir) adını verdi. Daha sonra diğerlerini ise alef-bir, alef-iki, alef-üç biçiminde sıralayacaktı. Keşiflerinin bir sonucu olarak Cantor, doğal sayıların toplama ve çarpma işlemlerini kendi tanımladığı sonsuz kardinallerle eşitleyen bir sonlu ötesi aritmetik geliştirmişti.
Georg Cantor’un Anlaşılması Uzun Zaman Alacaktı

Küme teorisinin bazı sonuçları gerçekten şaşırtıcı ve mantığa aykırıydı; Cantor’un birden fazla kez Dedekind‘den kanıtlarını gözden geçirmesini istemesinin nedeni de buydu. Ayrıca diğer şüpheci matematik meslektaşlarını ikna etmek için de çok çaba harcaması gerekiyordu.
Cantor’u en çok eleştiren kişi, Berlin Üniversitesi’ne girmesini engelleyen Leopold Kronecker’di. Kronecker matematiğin tam sayılara dayanması gerektiğini savunuyordu. Bu nedenle de matematiğin bu yeni başlangıç dalını sistematik olarak reddetti. Kronecker’in saldırıları Cantor’un hayatının geri kalanında periyodik olarak yaşayacağı sinir krizlerinin ilkini tetikledi. Devamında da bir hastanede tedavi olmak zorunda kaldı.

Cantor, bir daha da matematik yapacak kadar iyileşmedi. Fakat hastanede olmadığı dönemlerde de boş durmadı. 1890 yılında Alman Matematik Derneği’ni kurdu ve ilk başkanı seçildi. Matematik yapacak kadar iyileşmeyi beklerken bugün hâlâ tartışma konusu olan bir konuya ilgi duydu. Shakespeare diye birisinin olmadığı, tüm o oyunları Francis Bacon’un yazdığı iddialarını destekleyen makaleler yazdı.
1912’de St Andrews Üniversitesi’nden fahri doktor unvanını aldı, ancak hastalığı nedeniyle şahsen diplomayı kabul edemedi. Georg Cantor, 1913’te yoksul ve sağlığını yitirmiş bir biçimde emekli oldu. 1917’de Almanya’nın Halle kentinde bir psikiyatri kliniğinde yaşamaya başladı. Sonrasında da 6 Ocak 1918’de kalp krizi sonucu burada öldü.
Cantor’dan geriye zamanının çok öncesinde matematik dünyasına tanıtılmış bir sonsuzluk kavramı ve kümeler kuramı kaldı. Onun küme teorisi modern matematiğin çeşitli dallarında kullanılan ortak dil haline geldi. İnsanlık onun kapısını açtığı sonsuzluğu, ünlü matematikçi Hilbert’in şu sözleriyle hatırlayacaktı. “Hiç kimse bizi Cantor’un kapısını açtığı cennetten kovamayacaktır. “
Kaynaklar ve ileri okulamalar:
- Alfred S. Posamentier and Christian Spreitzer; The Lives and Works of 50 Famous Mathematicians
- Georg Cantor; Bağlantı: https://famous-mathematicians.com/
- Georg Cantor, the Man Who Discovered Different Infinities. Yayınlanma tarihi: 29 Mayıs 2019. Bağlantı: https://www.bbvaopenmind.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









