
Pi sayısını hesaplamak için bildiğimiz klasik metotların yanında fazla bilinmeyen bir kaç metot daha vardır. Bunlardan muhtemel en ilgi çekici ve alışılmadık bir yöntemi Eastern Illinois Üniversitesi’nde matematikçi olan Gregory Galperin, tarafından 2003 yılında keşfedildi. Bu yazıda çarpışan toplar yardımı ile pi sayısını hesaplamayı öğrenelim.
Bu ideal senaryoda, sürtünmesiz düz bir masa üzerinde sırasıyla m ve M kütlelerine sahip iki bilardo topu vardır. Daha küçük olan m kütleli top, bir bariyer ile büyük M kütleli topun arasındadır. Ve bu çarpışan toplar yardımıyla da pi sayısının basamaklarını hesaplamak mümkündür.
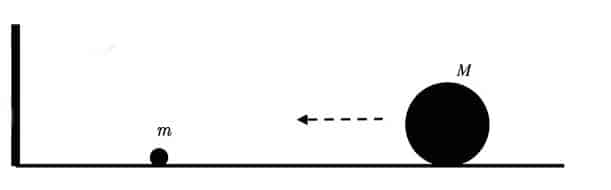
Şimdi büyük topu küçük olana doğru hareket ettirelim ve bu sayede ikisinin çarpışmasını sağlayalım. İki top çarpıştığı zaman tahmin edeceğiniz gibi, büyük olan biraz yavaşlayacak küçük olan da hareket etmeye başlayacaktır. Ancak bu çarpışmanın elastik bir çarpışma olduğunu kabul ediyoruz.
Bir elastik çarpışma, çarpışmanın sonucunda sistemdeki kinetik enerjide net kayıp olmayan bir çarpışmadır. Çoğu çarpışmada momentum korunur, ancak kinetik enerji korunmaz. Ancak elastik çarpışma adı verilen özel çarpışmalarda hem momentum hem de kinetik enerji korunur. Yani çarpışma sonucunda herhangi bir enerji kaybı yaşanmaz. Bundan sonra ne olacağı, m ve M kütlelerinin oranına yani M / m’ye bağlıdır.
Çarpışan Toplar ile Pi Sayısı Hesaplaması Nasıl Yapılır?
Şimdi, neyin ortaya çıktığını görmek için birkaç basit durumla başlayalım ve çarpışmaları sayalım. İki kütlenin oranı burada can alıcı faktör olduğundan, oranın logaritmasını alalım ve ona bir isim verelim: N=log100 M/n ( Buradaki 100 tabanı hesaplamada bazı kolaylıklar sağlaması açısından kullanılmıştır.)
Eğer iki kütle eşitse, yani M = m, o zaman oranları 1’e eşittir. Bu durumda kaç çarpışma vardır? Fizik kanunlarına göre, hareket halindeki sağ taraftaki top hareketsiz topa çarptığında (= 1 çarpışma), tüm hızını hareketsiz olana verir, dolayısıyla durur.
Önceden hareketsiz olan top sonuç olarak sola doğru hareket edecek ve duvara çarpacak (= 2 çarpışma), diğer topa vurmak için geri sekecek (= 3 çarpışma) ve ikincisini sonsuza kadar sağa doğru yola koyacaktır. Yani, toplam üç çarpışmamız olur. Bu durumda N=log100 M/n= log100 1=0 olacaktır.
Eşit kütleler yerine, M = 100 × m yapalım, böylece büyük kütle küçük olanın 100 katı olsun. Bu durumda, toplam çarpışma sayısının 31 olacağı ortaya çıkıyor. Bu bir bilgisayar simülasyonu ile doğrulanabilir, ancak aynı zamanda Galperin’in matematiksel olarak kanıtladığı şeyin bir sonucudur. Şimdi N=log100 M/n= log 100 (100/1)=1 oldu.
Aslında kütle oranını daha da artırarak işe devam edebiliriz. Örneğin şimdi daha büyük bilardo topunun kütlesini M = 10.000 × m olarak alalım. Bu elbette devasa bir bilardo topu. Ancak unutmayalım. Bu sadece idealize edilmiş bir durum, o yüzden oynamaya devam edelim.
Bu durumda, N=log100 M / n= log 100 (10000/1)=2 olur ve toplam çarpışma sayısı 314 olarak hesaplanabilir. Görmüş olduğunuz gibi, 100 sayısının katları olacak biçimde bilardo toplarımızın boyutlarını arttırırsak aşağıdaki tabloda göreceğiniz sonuçlar ortaya çıkacaktır.
Çarpışmalar Sonucu Elde Edeceğimiz Sonuçlar
| N | Toplam Çarpışma Sayısı | Pi sayısının Basamak Sayısı (N+1) |
| 0 | 3 | 1 |
| 1 | 31 | 2 |
| 2 | 314 | 3 |
| 3 | 3141 | 4 |
| 4 | 31415 | 5 |
| 5 | 314159 | 6 |
Çarpışan topların bir şekilde π sayısının rakamlarını üretebilmesi oldukça şaşırtıcı. Bu durumun sadece kullandığımız topun yuvarlak olmasıyla bir ilgisi olabileceğini düşünüyorsanız, yanılırsınız. Çünkü aynı senaryo kübik bloklarla değiştirilirse de argüman aynı şekilde çalışıyor. Kısacası yeterli topunuz varsa, pi sayısının istediğiniz kadar basamağını hesaplayabilirsiniz.
Yalnız hatırlatalım. Ağır top olarak Dünya’yı, hafif top olarak da küçük bir kum tanesini alsak, Pi’nin ancak ilk 15 basamağını elde ederiz. Yani bu yöntem Pi sayısını hesaplamak için elbette efektif bir yöntem değildir. Yine de denemek isteyenlere şimdiden kolay gelsin. Hesaplamalar hakkında daha fazla detaya erişmek isterseniz kaynaklar kısmına göz atmanızı öneririz. Ayrıca göz atmak isterseniz: Pi Sayısını Hesaplamak İçin Eğlenceli Ve İlginç Öneriler
Kaynaklar ve İleri Okumalar:
- The most unexpected answer to a counting puzzle; yayınlanma tarihi:13 Mart 2019; Bağlantı: https://www.youtube.com
- Calculate Pi Yourself Using Two Colliding Balls; Yayınlanma tarihi: 14 Mart 2019; Bağlantı: https://www.wired.com
- Pi Day: How to calculate pi using a cardboard tube and a load of balls; Bağlantı: https://www.newscientist.com/
- Urban Maths: Computing Pi – Inefficiently!; Bağlantı: https://ima.org.uk/
- Pi and Bouncing Balls – Numberphile; Bağlantı: https://www.youtube.com/watch?v=abv4Fz7oNr0
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel









