İskenderiyeli Öklid, 2000 yıldan fazla bir süre önce yaşamış ve genellikle geometrinin babası olarak anılan bir Yunan matematikçidir. Kaleme aldığı Elementler isimli kitabı şimdiye kadarki en başarılı kitaplardan biridir. Bu kitap aynı zamanda geometri tarihinin bilinen en eski sistematik tartışmasına neden olmuştur. Bu tartışma günümüzde Beşinci Aksiyom krizi olarak adlandırılmaktadır.
Öklid, içeriğinden çok konuları sunuşu açısından önemli olan bu eserinde bir takım tanımlar, aksiyomlar ve postulatlar ortaya koymuştu. Böylece Öklid geometrinin temellerini belirli tanım ve ilkeler çerçevesinde yapılandırmış oldu. Bu nedenle kendisi günümüzde aksiyomatik sisteminin kurucusu olarak kabul edilmektedir.
Öklid’in Aksiyomları Nelerdir?
Öklid, kitabında nokta, çizgi, yüzey ve cisim gibi geometrik kavramları tanımladıktan sonra kitaptaki derlemelerin tutarlı olmasını sağlamak için ‘kanıt gerektirmeyen apaçık gerçekler’ diye nitelediği beş aksiyomu sıraladı.
Öklid, aksiyomlardan sonra ‘ispat edilmeksizin doğru olarak benimsenen önerme, ön doğru’ anlamına gelen postulatlarını sıraladı. (Günümüzde tüm önermelere sadece aksiyom adını veriyoruz.). Öklid’in postulatları şöyleydi:
- İki nokta arasını birleştiren en kısa yol bir doğrudur. (İki noktadan bir ve yalnız bir doğru geçer.)
- Bir doğru iki yöne de sonsuza kadar uzatılabilir.
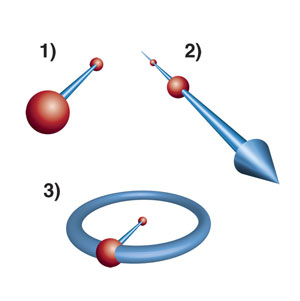
- Bir nokta ve bu noktadan başlayan bir doğru parçası verildiğinde, yarıçapı verilen doğru parçası ve merkezi verilen nokta olan bir çember çizebilirsiniz.
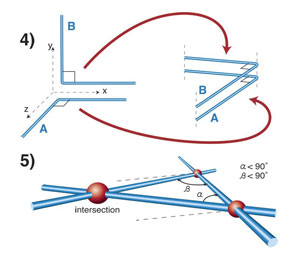
4. Bütün dik açılar birbirine eşittir. (Bu ifade oldukça anlamsız gelecektir. Sonucunda dik açı 90 derecelik bir açıdır ve 90 derecelik açıların tümü eşittir. Ancak Öklid’in dik açıları derece veya başka bir açı ölçüsü ile tanımlamadığını (onda yoktu) düşündüğümüzde bu gerçeği belirtme ihtiyacını anlayabiliriz.)
5. Eğer bir doğru parçasını, iki doğrunun üzerinden geçecek şekilde çizerseniz ve aynı tarafta doksan dereceden daha az iki açı oluşursa, o zaman bu iki doğru kesişir. (Bu önerme bir üçgenin açılarının 180 derece olacağını söylemekle eş değerdir.). Son iki önermenin nasıl göründüğünü aşağıda inceleyiniz.
Öklid’in aksiyomlarıyla yapabileceğiniz pek çok güzel şey var. Örneğin, düzgün bir altıgen çizebilirsiniz
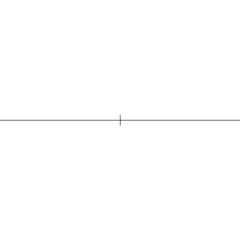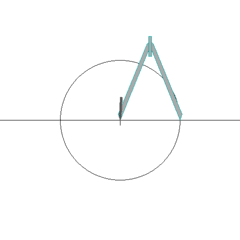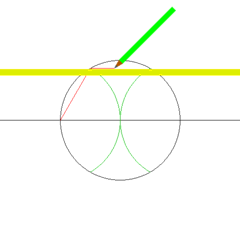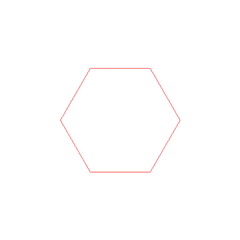
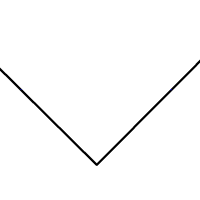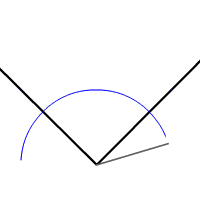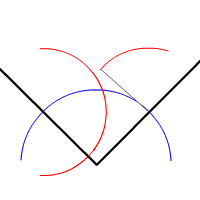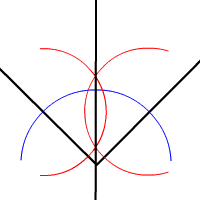
Veya bir açıyı iki eşit açıya bölebilirsiniz:
Beşinci Aksiyom İle İlgili Sorun Nedir?
Bununla birlikte, beşinci aksiyom matematikçilere bazı problemler yaşattı. Öklid, ilk 28 teoremini kanıtlamak için beşinci önermesine ihtiyaç duymamıştı. Kendisi de dahil olmak üzere birçok matematikçi, beşinci aksiyomun aslında sadece ilk dört önerme ile kanıtlanabileceğini düşünüyordu.
Matematikçiler ilk dört aksiyomu kullanarak beşincisini kanıtlamaya çalıştılar. Ancak, beşinci aksiyomu bir teorem olarak kanıtlamaya yönelik tüm girişimler başarısız oldu. Sonucunda matematikçiler beşinci aksiyomu daha kolay anlaşılır bir başkasıyla değiştirme ihtiyacı duydular.
İskoçyalı matematikçi John Playfair ( 1748-1819) beşinci aksiyoma mantıksal açıdan denk başka biçimde ifade etti. “Bir doğruya dışındaki bir noktadan sadece bir paralel doğru çizilebilir.” Aşağıdaki şekil Playfair Aksiyomu’nun görsel ifadesidir.
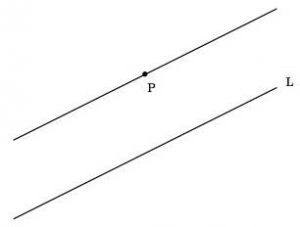
Playfair’in önermesinden sonra beşinci aksiyom genellikle Paralellik Aksiyomu adıyla anılmaya başlandı. Sonraki 1500 yılın büyük bir bölümünde birçok matematikçi Paralellik Aksiyomunu kanıtlamaya çalıştı. Matematikçiler yüzlerce yıl bu ispatla uğraştı. Hatta bazıları bu uğurda yaşantılarını harcadı. Bunun örneklerinden biri Janos Bolyai’nin hikayesidir. ( Merak ederseniz: Matematikçilerin İspat Takıntısı Ve Janos Bolyai’nin Kısa Hikayesi)
18’inci yüzyılın sonlarına doğru matematikçiler ilk kez Paralellik Aksiyomunun belki de diğer dört aksiyomdan hareketle kanıtlanmayacağını düşünmeye başladılar. Sonrasında da Öklid’in aksiyomuna bağlı olmayan bir geometri geliştirme çalışmaları başlayacaktı.
Beşinci Aksiyom Krizi Öklid Dışı Geometrileri Keşfetmemizi Sağladı
Carl Friedrich Gauss (1777-1855), Janos Bolyai (1802-1860), Nikolai İvanoviç Lobaçevski (1793-1856) gibi matematikçiler sonucunda Öklid dışı geometrilerin doğmasına önayak oldular. Öklid dışı geometrilerin keşfi, sadece matematik değil düşünce tarihinde de bir dönüm noktası olarak kabul edilmektedir.
1829’da Rus matematikçi Nicolai Lobachevsky, On the Principles of Geometry (Geometrinin İlkeleri) adlı kitabını yayınladı. Kendisi paralellik varsayımını yanlışlayan bir geometri hayal etti. Ondan birkaç yıl önce, Macar matematikçi Janos Bolyai’de benzer bir Öklid dışı geometri üzerinde çalışmıştı.
Beşinci Aksiyom Öklid Dışı Geometrilerde Nasıl Yorumlanır?
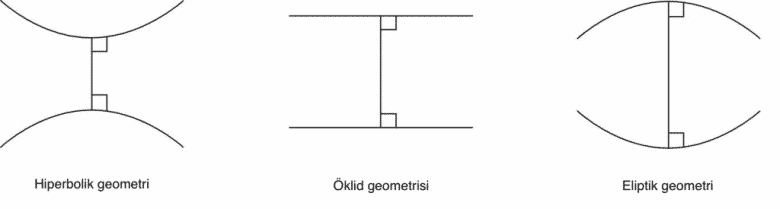
Bernhard Riemann’ın yaptığı da, Bolyai ve Lobachevsky’nin bulgularını genelleştirmek oldu. Günümüzde Lobaçevski geometrisi (hiperbolik geometri) ve Riemann geometrisi (eliptik geometri) olarak adlandırılan iki Öklid-dışı geometride Paralellik Aksiyomu şu şekilde yorumlanır.
- Düz bir yüzeyde bu noktadan geçen ve doğruya paralel olan yalnızca tek bir doğru vardır.
- Küresel bir yüzeyde bu noktadan geçen ve doğruya paralel olan hiçbir doğru yoktur.
- Hiperbolik yüzeyde bu noktadan geçen ve doğruya paralel olan sonsuz sayıda doğru vardır.
Bu sayede içinde yaşadığımız evrenin geometrisini yani küresel geometriyi anlamamız mümkün olmuştur. Bir kürenin yüzeyindeki iki nokta arasındaki en kısa mesafe düz bir çizgi değildir. Bunun yerine, kürenin yüzeyinde bulunan daire yaylarının parçasıdır.
Şimdi küre üzerinde aynı doğru üzerinde olmayan yani aynı yayda bulunmayan üç nokta alalım. Daha sonra bu noktaları birleştirelim. Şimdi aşağıda kırmızı çember parçalarıyla oluşturulmuş üçgene bakalım. Üçgenin köşelerinde kırmızı çember parçaları 90 derecelik açılarla kesişir. Dolayısıyla küresel geometride iç açıları toplamı 270 derece olan bir üçgen çizebiliriz.
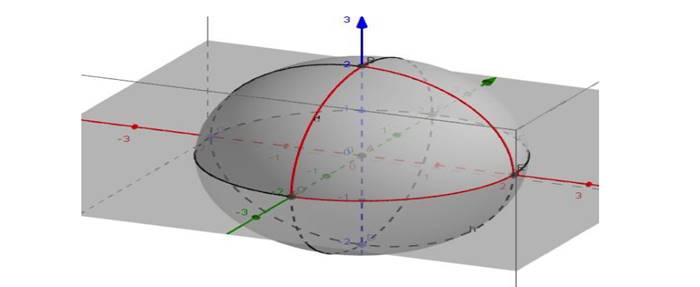
Küresel geometri bizi eğrilik kavramına götürür. Eğriliği anlamanın en basit yolu, üçgenlerin davranışını dikkate almaktır. Sıfır eğrilikteki bir yüzeyde bir üçgenin iç açılan toplamı 180 derece, pozitif eğrilikteki bir yüzeyde açıları toplamı 180 dereceden büyük, negatif eğriliği olan bir yüzeyde ise açılar toplamı 180 dereceden küçüktür.

Peki, bir yüzey negatif eğrilikte nasıl olur? Bir başka değişle açılarının toplamı 180 dereceden küçük olan üçgenler nerededir? Bir paket Pringles açın cevabı göreceksiniz. Cevabımız Hiperbolik geometridir. ( Göz atmak isterseniz: Üçgenin İç Açıları Toplamı Hep 180 Derece Olmaz: Hiperbolik Geometri)
Öklid dışı geometrilere uzun süre işe yaramaz gözüyle bakılsa da Einstein, içinde yaşadığımız üç boyutlu uzayın Öklid geometrisine değil, Öklid dışı geometriye uyduğunu gösterince düşünceler değişmiştir. Öklid dışı geometriler, insanın geometriyi doğru bir biçimde anlama, fiziksel uzayın gerçek niteliğini keşfetme girişimleri açısından hayati önemdedir.
Kaynaklar ve ileri okumalar
- Maths in a minute: Euclid’s axioms. Yayınlanma tarihi: 6 kasım 2014; bağlantı: https://plus.maths.org/
- Maths in a minute: Not always 180. Yayınlanma tarihi: 3 temmuz 2013; Bağlantı: https://plus.maths.org
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel