Dönem dönem manşetlerde karşınıza asal sayılar ile ilgili haberler çıkar. Matematikçiler yeni bir asal sayı keşfettiklerini heyecanla aktarırlar. Konuya yabancı olan birinin aklına bu durum karşısında ister istemez şu soru gelir. “İyi de bu benim ne işime yarayacak?” Eğer siz de bu kişilerden birisi iseniz okumaya devam ediniz. Bu yazıda “Asal sayılar nedir ve neden önemlidir?” sorusunun cevabını anlamaya çalışalım.

Matematikçiler asal sayıları genellikle matematiğin atomları olarak isimlendirirler. Bunun nedeni tüm sayma sayıların temelinde asal sayıların çarpımı ile oluşturulmasıdır. Mesela 12=2x2x3 biçiminde yazılabilir. Bu sayılara bileşik sayılar denir. Bazı sayıları ise ayırmak mümkün değildir: 2, 3, 5, 7, 11, 13, … Bunlara da asal sayılar veya kısaca asallar denir.
1 sayısı asal değildir, dizi 2’den başlar ve 3, 5, 7, 11, 13, 17, 19… biçiminde devam eder. Bir sayısının neden asal olmadığı genellikle merak edilmektedir. Detayları bu yazıda okuyabilirsiniz: Bir Sayısı Neden Asal Sayı Değildir?

Aslına bakarsanız “Asal sayılar nedir? sorusu uzun zamandır matematikçilerin kafasını meşgul etmekteydi. Eski Yunanlılar, asal sayıların birçok özelliğini anlamışlardı. 2300 yıl önce de kendisini daha çok geometriye yaptığı katkılar ile tanıdığımız Öklid, asal sayıların sonsuz sayıda olduğunu göstermişti. (Öklid’in Asal Sayıların Sonsuzluğuna Dair İspatı). Günümüzde bildiğimiz en uzun asal sayı 24.862.048 basamaklı 282.589.933-1 dir.
Eratostenes’in Kalburu Asal Sayıları Anlamak İçin Elimizdeki En Etkili Araçtır
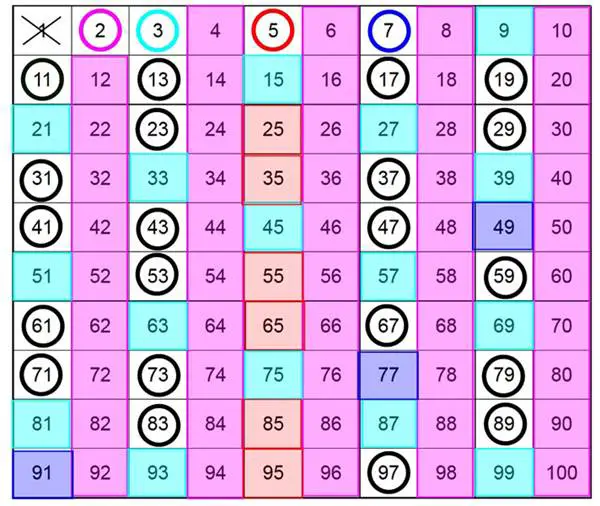
Asal sayıları incelemek için matematikçiler, yalnızca asallar kalana kadar tam sayıları birbiri ardına bir sanal ağ üzerinden eliyorlar. Bu eleme işlemi sayesinde günümüzde bilgisayarlar bir saniyeden daha kısa sürede milyarlarca asal sayı bulabiliyorlar.
Ancak elek fikrinin ana fikri 2000 yılı aşkın süredir değişmedi. Bu konuda bize bir fikir veren ilk kişi Eratosthenes olarak bilinmektedir. Aslında bu fikri hemen hemen her ilk öğretim öğrencisi de bilir. Görünümü aşağıdaki gibi olmaktadır.
Daha Büyüklerini Bulma Çabaları
Asal sayıların listelenmesi konusunda dikkate dönük bir çaba harcayan ilk kişi İngiliz bir matematikçi olan John Pell ( 1611-1685) olarak bilinir. 1700’lerin başında 100.000’e kadar olan asal sayıları hesaplamayı başarmıştı. 1800’e gelindiğinde ise bu sayı 1 milyona ulaşmıştı. 1800’lerin ortalarında, matematikçi Jakob Kulik, 100 milyona kadar olan tüm asal sayıları buldu. Bunun için yine Eratosthenes kalburunu kullanıyordu. Ancak gözlemlediği bazı şablonlar sayesinde işi biraz hızlandırmıştı.
Ancak tüm bu çabalar, Carl Friedrich Gauss asal sayıları analiz etmeye karar vermemiş olsaydı, yalnızca bir referans tablosu işlevi görebilirdi. Gauss sayılar ile incelemeler yaptıktan sonra, Gauss, asal sayıların giderek daha az sıklıkta karşımıza çıktığını fark etti. Gauss’un ilk keşfinden bir asır sonra, bulguları “asal sayılar teoremi” ile kanıtlandı.
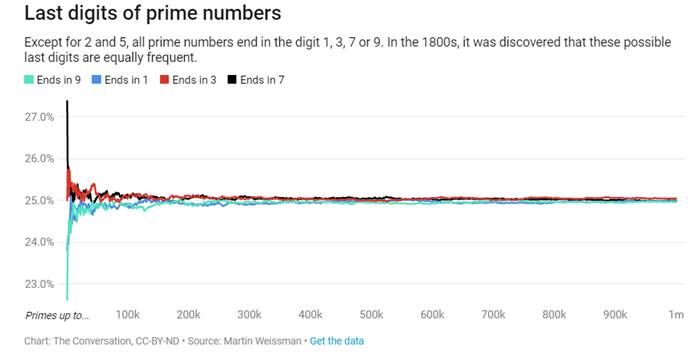
Bugün hesaplamalar bilgisayarlar aracılığı ile yapılsa da matematikçiler yeni şablonlar bulmaya devam ediyorlar. Örneğin, 2 ve 5 hariç tüm asal sayıların sonu 1, 3, 7 veya 9’dur. 1800’lerde bu olası son rakamların eşit sıklıkta olduğu kanıtlanmıştır. Başka bir deyişle, bir milyona kadar olan asal sayılara bakarsanız, yaklaşık yüzde 25’i 1, yüzde 25’i 3, yüzde 25’i 7 ve yüzde 25’i 9 ile biter.
En Büyük Asal Sayı Sürekli Değişiyor, Bunu Nasıl Buluyoruz?
En büyük asal sayı arayışının ardında yatan neden elbette sadece bir rekoru elde tutmak değildir. Büyük sayılar pratikte çok önemlidir. Bu durumda verilen bir sayının asal çarpanlarına ayrılması ile ilgilidir. Küçük bir sayının çarpanlarına ayrılması kolaydır. Ancak sayı büyüdükçe bu durum zorlaşmaya başlar. Bu nedenle daha büyük asal sayılar daha fazla güvenlik demektir. Asal sayıların şifreleme tekniklerinde kullanılmasının sebebi de işte budur.

Baştan beri dediğimiz gibi asal sayılar sonsuzdur. Bu nedenle en büyük asal sayı diye bir şey yoktur. 1996 yılından beri bu sayıları arama işi Mersenne Prime Search (GIMPS) tarafından sürdürülüyor. Hatta bu arayışa sizler de dahil olabiliyorsunuz. Tek yapmanız gereken bilgisayarınıza küçük bir program indirip bir sayının Mersenne Asalı olup olmadığını kontrol etmek olacaktır. Bu noktada da akla gelen soru elbette Mersenne Asalının ne olduğu oluyor.
Mersenne Asalları İle Asal Sayıların İlişkisi
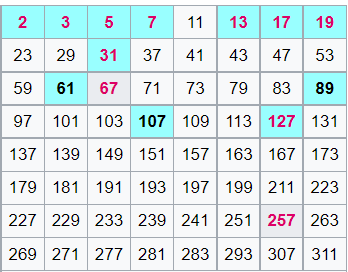
Günümüzde p doğal sayısı için 2p – 1 şeklindeki sayılara Mersenne sayıları, bunların asal olanlarına da Mersenne asalları denir. Sebebi, Mersenne’in 1644 tarihli Cogitata Physica-Mathematica adlı eserinde 257’ye kadarki tüm p değerlerinden sadece p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 ve 257 değerlerinin bize asal sayı verdiğini iddia etmesidir. Bugün Mersenne’in beş hata yaptığını biliyoruz. İlk olarak p = 67 ve 257 için Mersenne sayıları bileşik sayıdır. Ayrıca listede yer almayan p = 61, 89, 107 gibi üç asal sayı da Mersenne Asalıdır.
Zaman geçtikçe işin içine bilgisayarlar karıştı. Bunun sonucunda daha fazla Mersenne Asalı ortaya çıktı. Bu tür sayıların asal sayı olup olmadığını kontrol etmek için çok hızlı ve özel yöntemler ortaya kondu. Bunlardan biri Lucas-Lehmer testi olarak bilinmektedir. Bu algoritma ve bilgisayar yardımı ile büyük asal sayı avına çıkabiliriz.
Asal Sayılar Neden Bu Kadar Önemlidir?
Çok uzun bir süre boyunca, asal sayılar ancak matematikçiler için önemliydi. Asal sayıların gerçekten önemli hale geldiği ilk an, 1970’lerde, asal sayıların açık anahtarlı kriptografi algoritmalarının temeli olarak hizmet edebileceğinin ilk duyurulduğu zamandı. Günümüzde şifreli bir mesaj göndermek için interneti her kullandığınızda asal sayılara dayalı bir algoritma kullanıyorsunuz.
Asal sayılar ayrıca kuantum mekaniği ve soyut cebir gibi alanlarda da önemli rol oynar. Aslına bakarsanız, asal sayılara hiç beklemediğimiz yerlerde de rastlayabiliriz. Örneğin Magicicada cinsi ağustos böcekleri, zamanlarının çoğunu toprak altında kurtçuklar olarak geçirirler. 7, 13 veya 17 yıl sonra ortaya çıkarlar. Ve bu sayıların hepsi asal sayılardır.
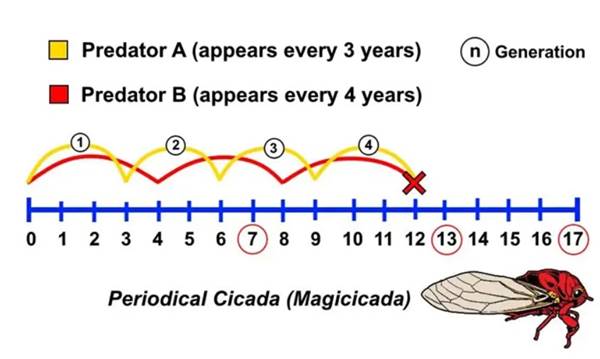
Eğer, bu ağustos böceklerinin 12 yıllık yaşam döngüleri olsaydı, 1, 2, 3, 4 veya 6 yıllık yaşam döngülerine sahip olan diğer türler tarafından bulunmaları ve avlanmaları çok daha kolay olabilirdi.
Asal sayılar ile ilgili bu noktaya kadar aktardıklarımız sadece bir ön bilgi niteliğindedir. Bu sayılar ile ilgili daha bir çok gizem çözümsüz olarak beklemektedir. Örneğin, asal sayıların sayı doğrusu boyunca nasıl dağıldığıyla ilgili olan Riemann hipotezi, herhangi bir çözümün 1 milyon dolar değerinde olduğu yedi büyük “milenyum probleminden” biridir.
Kaynaklar ve ileri okumalar için:
- Why should we care about prime numbers?; https://mashable.com/
- Why Prime Numbers Still Surprise and Mystify Mathematicians; Yayınlanma tarihi: 2 Nisan 2018; Bağlantı: https://www.smithsonianmag.com
Matematiksel