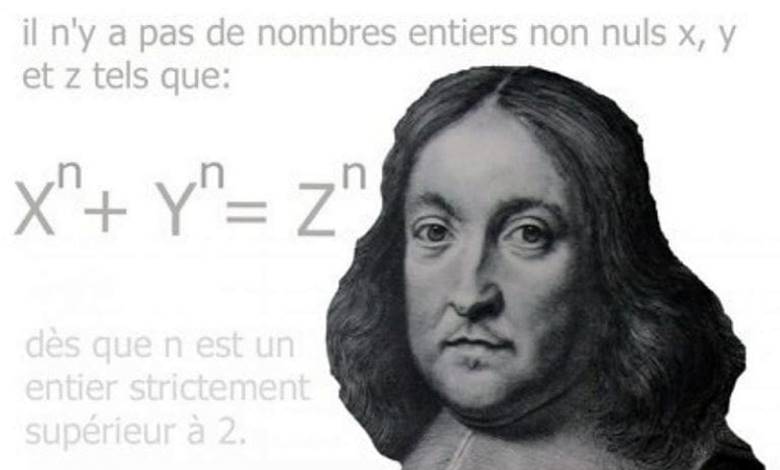
Pierre de Fermat “Amatörlerin Prensi” olarak tanınır. Bunun en önemli nedeni, adını günümüze kadar taşıyan Fermat’ın Son Teoremidir. Fermat’ın son teoreminin en iyi yanı, teoremi anlamak kolaydır. Ancak iş ispatlamaya geldiğinde aynı şey söylenemez. Hatta o kadar zordur ki, üstesinden gelmek için dünyanın önde gelen matematikçileri 350 yıl boyunca bu soruyla uğraşmıştır.
Aslında her şey 1650 yılı civarında Fermat’ın Diophantus’un Arithmetica adlı kitabının kenarına gizemli bir not düşmesi ile başladı. “… Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet!”. Bu şunun gibi bir anlama gelmekteydi. “Teoremin müthiş bir kanıtını buldum fakat burada yazacak kadar yer yok”.
Diophantus MS 250 yılı civarında çözümleri kesirler ya da tamsayılar olması gereken denklemler ile ilgili bir kitap yazmıştı. Bu denklemlere günümüzde Diophantus denklemleri denir. Diophantus kitabında tüm Pisagor üçlülerini bulmak için genel bir kural yazmıştı.
Pierre de Fermat profesyonel bir matematikçi değildi. Günlük işi hukuk danışmanlığıydı. Ama tutkusu matematik özellikle de günümüzde sayılar kuramı adını verdiğimiz tamsayıların özellikleri ile uğraşmaktı. İşte Fermat notunu tam da Pisagor üçlüleri ile ilgili kısmın yanına yazmıştı. Muhtemel Pisagor üçlüleri hakkında düşünmüş ve bunu genellemenin bir yolunu aramıştı.
Fermat’ın Son Teoremi Bize Ne Anlatır?
an + bn = cn
Yukarıdaki denklemde n yerine 2 yazdığımızda bu denklem Pisagor teoremine dönüşür. Sonuçta bildiğimiz gibi bu denklemi sağlayan a,b,c tamsayıları mevcuttur. Bunlar Pisagor üçlüleridir. Bu denklemde n yerine 3 yerleştirdiğiniz vakit işler o kadar kolay olmaz.
Çünkü 0 sayısı hariç denklemi sağlayan a, b, c tamsayılarını bulmak kolay değildir. Aynı sorun n=4 için de geçerlidir. 5 ve 6’da da çözüm yoktur. İşte tüm bu denemelerden sonra Fermat pes etmiş olmalı ki meşhur notuyla aslında bize şu mesajı yolladı:
” Bir küpü, iki küpün toplamı, bir dördüncü üssü iki dördüncü üssün toplamı genel anlamda ikiden daha büyük herhangi bir üssü aynı türden iki üssün toplamı olarak çözümlemek imkansızdır.”
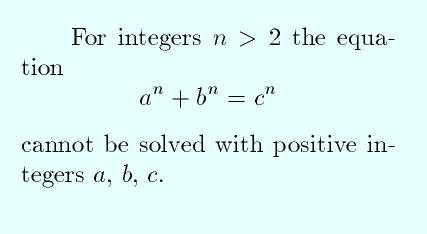
Fermat’ın yanına not düştüğü bu kitap yıllar sonra oğlu tarafından fark edildi,. Devamında kitabın yeni baskısı içindeki notlarla birlikte yapıldı. O zamandan sonra bu kitabı okuyan matematikçiler Fermat’ın iddialı sözüyle karşılaşınca hadi bizde deneyelim diye işe giriştiler. Sonunda Fermat’a meydan okuma yarışı başladı.
Aslında Fermat kitabın kenarlarına ispatı verilmemiş sayılar kuramı ile ilgili başka sorularda yazmıştı. Süreç içinde matematikçiler diğer tüm problemleri ispat ettiler. Sonunda geriye doğruluğu ya da yanlışlığı ispatlanamayan son bir teorem kaldı. Bu nedenle doğal olarak bu teorem Fermat’ın son teoremi olarak bilinmeye başlandı. Matematikçiler yıllar içinde bu teorem üzerinde çalışıp başarısız oldukça probleme ilgi arttı. Zamanla da bir fenomen haline dönüştü.
Fermat’ın Son Teoremi İçin Çözüm Arayışları
İlk çözüm küpler için böyle bir çözüm olmadığını söyleyen Euler’den geldi. Fermat’ın kendisi başka bir notunda dördüncü dereceden üsler için çözüm olmadığını ispatlamıştı. Peter Lejeune Dirichlet 1828’de beşinci ve devamında da 14. üsler için de çözümlerin kesin olmadığını doğruladı.
İlerleyen yıllarda bu çılgınlık zaman içinde durağanlaştı ve matematikçiler başka alanlara yöneldiler. Ancak 10 yaşında bir çocuk bir gün kütüphanede bu teoremin anlattığı bir kitapla karşılaşınca teoremin kaderi değişti. Andrew Wiles adlı bu çocuk için bu problem artık hayatının tutkusu halini alacaktı. Matematikçi olan Andrew bir gün Taniyama – Shimura hipotezi ile karşılaştı.
Bu hipotezin ispatı ile Fermat’ın son teoreminin ispatı arasında bir bağ olduğunu fark etti. Hikayenin devamını bu yazımızda ele aldık, oradan okumaya devam edebilirsiniz: Fermat’a Meydan Okuyan Bir Profesör: Andrew Wiles. Sonuçta macera tamamlandı. 1635-1637 arasında ileri sürülen bu teorem ancak 1994 yılında İngiliz matematikçi Andrew Wiles tarafından kanıtlandı.
Fermat’ın Son Teoremi ve Simpsonlar
Günümüzde halen bazı matematikçiler Fermat’ın son teoremi ile oynamayı seviyorlar. Simpsons izlemeyi sevenler aslında bu animasyonun bazı karelerine daha dikkatli bakarlarsa çeşitli yerlere serpiştirilmiş matematik ile karşılaşacaklardır.
Bunun sebebi bu animasyonun yapım ekibinde birçok matematikçinin yer alması ve tutkularını yaptıkları işe aktarmalarıdır. Bunun yanında elbette biraz da kafa karıştırmak istemeleridir. Bunlardan bir kaç tanesi aşağıda gördüğünüz karelerdir. ( Daha fazlası için: Simpsonlar Dizisinden Akılda Kalan Matematik Şakaları)
Bu tahtada yazan işlemin cep telefonlarınızla sağlamasını yapmaya kalkarsanız doğru. Neler oluyor? Andrew yanılıyor mu?
Aslında elbette değil bu sadece bir şaşırtmaca. Cep telefonlarımız veya klasik hesap makineleri sadece belli bir basamağa kadar işlem yapabilir. Bir bilgisayar yardımı ile verilen sayıları denerseniz çok yakın olduğunu ama tam olarak sağlamadığını görebilirsiniz. Herkesin kafasında bir soru var. Fermat bu teoremin ispatını daha kısa biçimde yapabilmiş miydi? İşte bu bir muamma. Fermat’ı biraz daha tanımak isterseniz tarafımızca çevrilen aşağıdaki videoya da göz atabilirsiniz…
Kaynak ve İleri izlemeler:
- Fermat’s Last Theorem – Numberphile; https://www.youtube.com
- The Bridges to Fermat’s Last Theorem – Numberphile; https://www.youtube.com
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel