Matematik, sayıların bilimidir ve tıpkı diğer bilim türleri gibi, sürekli olarak gelişmektedir. Bununla birlikte, yeni fikirler yarattığı çelişkilerden dolayı her zaman hoş karşılanmaz. Benzer bir şekilde, irrasyonel sayıların keşfi de yerleşik sayı doktrinlerine meydan okumuştu.
En ünlü irrasyonel sayı ise elbette bazen Pisagor sabiti olarak da adlandırılan karekök iki sayısıdır. Bu yazıda irrasyonel sayılar ile ilgili akıllara takılan bir kaç konu hakkında kısa bilgiler paylaşalım.
Rasyonel ve İrrasyonel Sayılar nedir?
Sayılar ve matematik için ilk temelimiz, bir şeyleri sayma ve ölçmeye yönelik pratik ihtiyaçtan kaynaklanmaktadır. Bu nedenle doğal sayıları kavramak kolaydır. Ölçülebilir miktarları daha küçük parçalara bölme ihtiyacı nedeniyle kesirler de mantığa uygun gelmektedir. Bu nedenle iki sayma sayısının oranı biçiminde yazılabilen sayılar bugün rasyonel sayılar olarak biliniyor.

Bunun karşıtı gibi gözüken “İrrasyonel sayılar” adı, kelimenin tam anlamıyla bu sayıların “mantıktan yoksun” olduğu anlamına gelmez. Aslında a/b biçiminde ifade edilemeyen herhangi bir sayı irrasyonel bir sayıdır. Bu nedenle karekök 2 bir irrasyonel sayıdır. Çünkü bu sayıyı bir kesir ile gösterme şansımız yoktur.
Pi Sayısı Rasyonel midir?
Bu arada merak edilen bir soru Pi sayısının irrasyonel bir sayı olup olmadığıdır. Bunun nedeni aslında okullarda pi sayısının 22/7 biçiminde öğretilmesidir. Sonuçta 22/7 rasyonel bir sayı olduğu için, pi sayısı da olmalıdır diye düşünülür. Ancak bu düşünce elbette yanlıştır.
22/7 pi sayısı ile işlem yapmaya kolaylaştırmak adına kullanılan yaklaşık bir değerdir. Pi sayısına eşit değildir. Zaten hiç bir sayı pi sayısına eşit olamaz. Pi sayısı ile ilgili daha fazla bilgiye bu yazımızdan erişebilirsiniz. Binlerce Yıldır Dünyayı Büyüleyen Pi Sayısı Hakkında Bazı İlginç Bilgiler
İnsanlar bu tür sayıların varlığından haberdar olsalar da, rasyonel sayıların tanımıyla çeliştikleri için Pisagor zamanında henüz kanıtlanamamıştı. Pisagor’un öğrencilerinden Hippasus tarihte “irrasyonel” sayıların varlığını kanıtlayan ilk kişi olarak kabul edilmektedir.

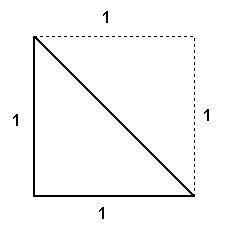
Hippasus dik kenar uzunlukları 1 birim olan bir ikizkenar dik üçgende Pisagor Teoremi uygulandığında hipotenüsün uzunluğunu veren, yani karesi 2’ye eşit olan sayının iki sayma sayısının oranı olarak ifade edilemeyeceğini keşfetti.
Kenarları 1 birim uzunluğunda olan karenin köşegeni karekök 2 birim uzunlukta idi. Yani yaklaşık 1.4142. Bugün için size bu sayı garip gelmeyebilir ancak o dönemde durum farklıydı. Ancak farklı bir sayı kümesinin varlığı dönemin mevcut inançları ile çelişmekteydi. Bu da aslında Hippasus’un sonunu hazırlamıştı.
Karekök 2 sayısı İrrasyoneldir dediğimizde ne demek İsteriz?
Örneğin Karekök 2 sayısını bir hesap makinası yardımı ile hesaplarsak 1.41421356237309504880… gibi bir sonuç elde ederiz. Dikkat ederseniz rakamlar arasında hiçbir tekrar bulunmamaktadır.
Şimdi aşağıdaki örneklere bakalım. 1/7=0.142857142857142857142857 … biçiminde bir sonuca sahiptir. Dikkatli bakarsanız 142857 rakam öbeği tekrarlamaktadır. Şimdide 1/109 kesrine bakalım.
1/109=0.0091743119266055045871559633027522935779816513761467889908256880733944954128440366972477064220183486238532110091743119266055045871559633027522935779816513761467889908256880733944954128440366972477064220183486238532110091743119266055045871559633027522935779816513761467889908256880733944955412844036697247706422018348623853211009174… biçiminde devam eder.
Kesrin ilk 100 basamağını hesapladığımızda herhangi bir tekrar görmeyiz. Bu, kesrin irrasyonel olduğu anlamına mı gelir? Hayır gelmez. Eğer hesaplamamızı 330 basamağa kadar götürürsek sayıda 108 rakamlı bir devir bulunduğunu buluruz. Oysa ki, bir irrasyonel sayıda böyle bir tekrar elde etmemiz mümkün değildir.
Hippasus’un Karekök 2 sayısı İçin yaptığı İspat

Kendisi işe √2 sayısının rasyonel yani iki sayma sayısının oranı olduğunu kabul ederek başladı. Her rasyonel sayı bir oran olarak ifade edilebildiğinden, √2, p / q biçiminde yazılır. Burada, p ve q tamsayıdır ve 1 dışında herhangi bir ortak bölene sahip değildir.
Denklemin her iki tarafının karesi alındığında p2/q2=2, yani diğer bir deyişle p2=2q2 olur. Tek sayıların karelerinin her zaman tek sayı verdiğini, çift sayının karesinin ise her zaman çift sayı verdiğini biliyoruz. Buradan anlıyoruz ki p sayısı bir çift sayıdır.
O zaman bir k tamsayısı için p=2k yazabiliriz. Şimdi bunu denklemde yerine yazalım. 2q2=(2k)2=4k2olur. Gerekli sadeleştirme sonucunda q2=2k2 ifadesi bulunur. Bu durumda q2‘nin, dolayısıyla q’nun da çift olması gerekiyor.
Ve işte burada işler karışıyor, sonuçta ikisi de çift sayı ise sadeleşebilmeliler oysa biz başlangıçta bu sayıların aralarında asal olduğunu yani sadeleşmediğini kabul etmiştik. Bu, başlangıçtaki “Karekök 2” nin rasyonel bir sayı olduğu varsayımımızın yanlış olduğu ve bu nedenle irrasyonel olması gerektiği anlamına gelir.
Hippasus Neden Öldü?
İrrasyonel sayıların keşfi, matematik adına önemli bir keşifti. Takip eden zamanda, tek doğru matematik bilimi sürekli büyüklükler arasındaki ilişkilerin çalışıldığı geometri olacaktı. Ancak değişim gelenekçiler için kolay değildir. Sonuçta bu keşif onların mutlak gerçeğinin karşısında duruyordu.
Yunan filozof Hippasus bir gün güney İtalya’daki evinden ayrıldı ve bir gemiye bindi. Hippasus’un neden seyahat ettiğini ya da nereye gideceğini bilmiyoruz ancak yapamadığını biliyoruz.
Efsaneye göre gemi kıyıdan uzaklaştığında, zavallı filozof Pisagor kardeşliğindeki dostları tarafından saldırıya uğradı ve denize atıldı. Pisagorcuların arkadaşlarına aniden saldırmaları için iyi sebepleri vardı. Sonuçta onlar Pisagor’un öğretilerini körü körüne takip eden kişilerdi. Efsane ya da değil kesin bilemeyiz ama gerçeklik payı kulağa olası gibi geliyor.
Ancak yine de sonuç değişmeyecekti. Hippasus’un keşfi batı matematiğinin akışını birçok yönden değiştirdi. Ayrıca göz atmanızı öneririz: Her şey Sayı mı Yoksa Geometri mi? Pisagor ve Eudoxus
Kaynaklar ve ileri okumalar:
- The Dangerous Ratio; Bağlantı: https://nrich.maths.org/2671
- A Brief History of Infinitesimals. The Idea That Gave Birth to Modern Calculus; Yayınlanma tarihi: 1 Nisan 2014; Bağlantı: https://www.scientificamerican.com/
- E. W. Weisstein. Irrational Number. Alındığı Tarih: 2 Kasım 2021. Bağlantı: https://mathworld.wolfram.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










Çok güzel yazılar yazıyorsunuz, sizleri kutluyorum. Yukarıdaki sayı kök 2 değil kare kök 2 olduğunu hatırlatma cüretinde bulunabilir miyim?
Haklısınız, uyarınız için teşekkürler.
Bu kadar çorak iklimde matematiğin aydınlık dünyasından kesitler sunduğumuz için teşekkür etmeyi bir borç bilirim.
Saygılarımla.