Matematikte bazı kavramları ezberler ve öylesine uygularız. Bunlardan bir tanesi de karşımıza faktöriyel tanımında çıkar. Konu ile ilk tanıştığımız zamanlarda sıfır faktöriyelin bire eşit olması gerektiği söylenir ve devamında da örnekler ile konuya devam edilir. Peki ama neden sorusu da çoğu zaman cevapsız olarak kalacaktır.

Pek çok matematiksel hesaplamada karşımıza çıkan faktöriyeller, n doğal sayıları için, n’den küçük veya ona eşit tüm sayıların çarpımını ifade eder. Örneğin 4! = 24 dendiği zaman 4 x 3 x 2 x 1 = 24 işleminin yapıldığını anlarız. Tanımlamada da 0!=1 ve 1!=1 dir.
İşte bu tanımda kafa karıştıran nokta sıfır faktöriyelin bire eşit olduğunu söyleyen ifadedir. 0 faktöriyel, içinde değer bulunmayan bir veri kümesini düzenleme yollarının sayısını bulmak anlamına gelmektedir. Peki ama neden sonucu bir çıkar?
Faktöriyellerin Genellemesi Gama Fonksiyonu İle Tanışalım
Öncelikle son söyleyeceğimizi ilk söyleyelim. Ortaöğretim sıralarında tanıştığımız faktöriyel gösterimi aslında işin sadece başlangıcıdır. Aşağıdaki görselde Gama fonksiyonunu görüyorsunuz. Sıfır faktöriyel neden bire eşittir sorusunun asıl cevabı bu fonksiyondur.
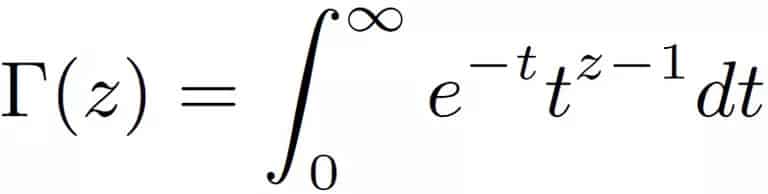
Gama fonksiyonu matematikte faktöriyel fonksiyonunun karmaşık sayılar ve tamsayı olmayan reel sayılar için genelleyen bir fonksiyondur. Bu tuhaf görünümlü fonksiyonu, Yunan alfabesinden büyük harf gamma ile şuna benzer Γ(z) bir biçimde yazarız. Bu fonksiyon ilk defa 1729 yılında matematikçi Leonhard Euler tarafından keşfedilmiştir.
Gama fonksiyonun bazı temel özellikleri vardır. Bunlardan bir tanesi Γ (z + 1) = z Γ (z) biçimindedir. Ayrıca Γ( 1 ) = 1 kabulümüz de vardır. Bu ikisini kullanarak Γ( z ) = ( z – 1) Γ( z – 1 ) = ( z – 1) ( z – 2) Γ( z – 2 ) = (n – 1)! sonucunu da elde edebiliriz. Bu sayede de Gama fonksiyonu ile faktöriyeller arasında bağlantı kurarız.
Şimdi Γ (z) = (z-1)! sonucunda sahibiz. Bu da bize Γ (1) = ( 1-1)!=0! sonucuna götürür. Yani sıfır faktöriyel değerinin neden 1’e eşit olduğunun asıl cevabını verir. Ondalık bir sayının faktöriyeli nedir sorusu, faktöriyellerin tanımı nedeniyle kulağa saçma gelir. Oysa ki gama fonksiyonu sayesinde bunu hesaplamak da mümkündür. Örneğin 2,5! yaklaşık olarak 1,329 değerine eşittir. 1,5! ise yaklaşık olarak 0,886 kadardır.
Sıfır Faktöriyel Nedir?
Yukarıda aktardığımız Gama fonksiyonu bize belli bir açıklama sunsa da sezgisel değildir ve temelinde bir öğrenciye bu biçimde açıklamak da kolay olmayacaktır. Bunun için yazının devamında soruyu başka bir bakış açısı ile cevaplamaya çalışalım. Bilindiği gibi faktöriyel kavramı permütasyon ve kombinasyon konularının temelini oluşturmaktadır.
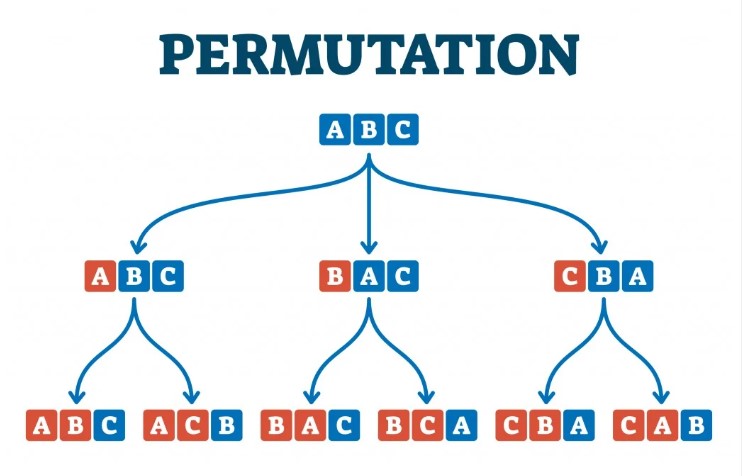
n! diye tanımladığımız şey aslında n tane farklı nesneyi kendi içinde nasıl sıralayabileceğimizin sayısıdır. Yani 3 tane farklı gömleğinizi bir rafa sıraya dizmek isterseniz bunu 3!=6 kadar şekilde yapabilirsiniz. Peki gömlek sayınız iki olursa. Elbette o zaman cevabınız 2!=2 olacaktır. Bir tanecik gömleğiniz varsa da o zaman üzgünüz sadece bulunduğu biçimde kalacaktır :) Yani 1!=1 olacaktır.
Eğer hiç gömleğiniz yoksa işin içine biraz felsefe karışıyor. “Hiç gömleğim yok, bunu kaç farklı biçimde sıralayabilirim?” Cevabınız elbette sıralayamam olacaktır ama unutmayın bu cevap matematikte boş kümeye karşılık gelmektedir. Ve bununda sayısal bir karşılığı vardır. Bu da bir olacaktır.
Sıfır faktöriyel neden Bir Yapar sorusunun İkinci Olası cevabı
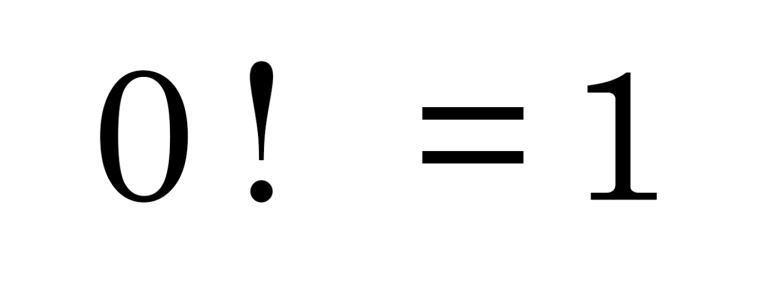
Sıfır faktöriyelin 1 olarak kabul edilmesi, matematiksel işlemlerin ve denklemlerin tutarlı bir şekilde işlemesine de yardımcı olur. Birazdan göstereceğimiz yöntem size sıfır faktöriyelin neden bir olduğunu açıklayamaz. Ancak neden bu biçimde kabul edilmesi gerektiği konusunda bize bir fikir verir.
Bir kombinasyon, sıraya bakılmaksızın bir kümenin öğelerinin gruplanmasıdır. Örneğin, {1, 2, 3} kümesini düşünün. Bu unsurları nasıl düzenlersek düzenleyelim, sonunda aynı üçlüye ulaşıyoruz. Bu nedenle kombinasyon hesabı için kullandığımız formül C (n,r ) = n!/[r!(n – r)!]. biçimindedir.
3 elemanlı bir kümenin 3’lü kombinasyonlarını hesaplamaya kalktığımızda da payda da (3-3)! biçiminde bir ifade oluşacaktır. Bu da 0!=1 ifadesini kullanmaya bizi zorlayacaktır.
Sonuç olarak 0 faktöriyelin 1 olmasının temel nedeni bunun bir kabul olmasıdır. Matematiksel hesaplamalarda bu kabulü kullanmak, birçok matematiksel ve istatistiksel özdeşliği korumaya yardımcı olur. Yazımızın devamında okumaya devam etmek isterseniz: Verilen Bir Sayıyı Neden Sıfıra Bölemiyoruz?
Kaynaklar ve ileri Okumalar:
- Taylor, Courtney. “Why Does Zero Factorial Equal One?” ThoughtCo, Apr. 5, 2023, thoughtco.com/why-does-zero-factorial-equal-one-3126598.
- Why Is The Factorial Of Zero Equal To One?. Yayınlanma tarihi: 8 Temmuz 2022. Bağlantı: Why Is The Factorial Of Zero Equal To One?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel